“自认为为他人好而做的事情并不一定是正确的。”,那是一篇充满了说教意味的故事。——《魔女之旅》
最短路
在
没错,就是最短路 !(屑之路)
最短路问题 ,是网络理论 解决的典型问题之一,可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。
基本内容是:若网络中的每条边都有一个数值(长度、成本、时间等),则找出两节点(通常是源节点和阱节点)之间总权和最小的路径 就是最短路问题。
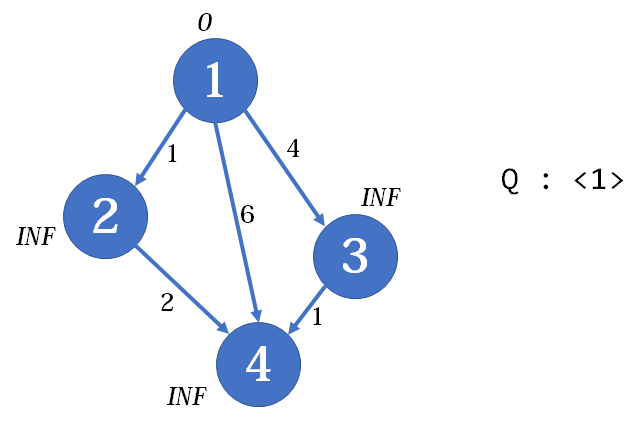
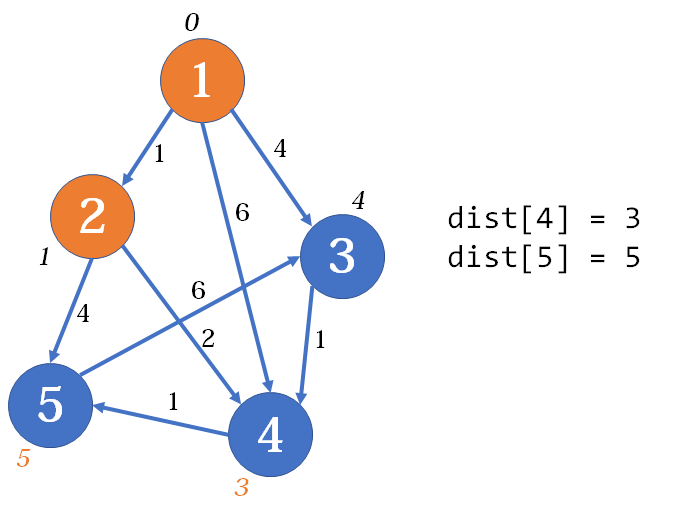
很明显,上面这张图里,从
最短路问题分为单源最短路 和多源最短路 。前者只需要求一个固定的起点到各个顶点的最短路径 ,后者则要求得出任意两个顶点之间的最短路径。
好,看完了这些我们来看看怎么解决最短路问题。
Floyd-Warshall 这是一个差劲的算法……算了,这是必要的牺牲,因为万事开头难(但似乎“万事开头难,然后中间难,最后结尾难”)。
Floyd算法 又称为插点法 ,是一种利用动态规划的思想 寻找给定的加权图中多源点之间最短路径 的算法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int dist[220 ][220 ];void Floyd (int n) for (int k = 1 ; k <= n; k ++) { for (int i = 1 ; i <= n; i ++) { for (int j = 1 ; j <= n; j ++) { dist[i][j] = min (dist[i][j], dist[i][k] + dist[k][j]); } } } }
讲道理,这个方法比较像找中间商,如果我要买个东西,我需要考虑是直接从官网买呢,还是找中间商会便宜一点呢,通过这种方法来找最短路。
给出几张图来模拟一下
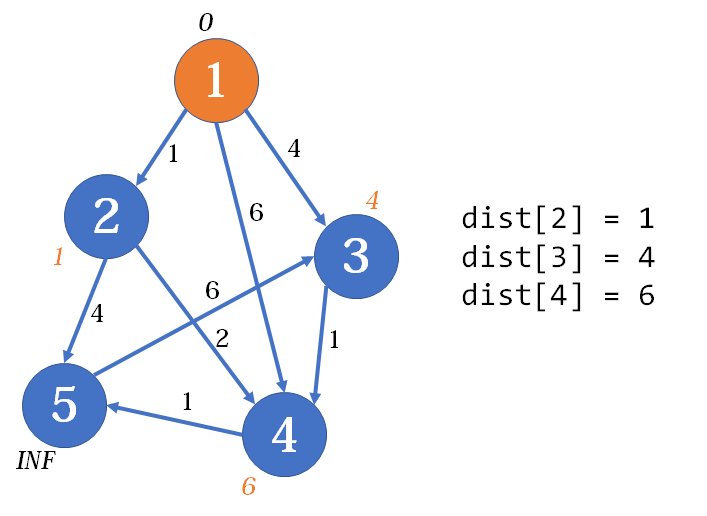
初始化是这样的:
先是初始化,因为用的是邻接矩阵一般的存图方法,
1 2 3 4 5 6 7 8 9 memset (dist, INF, sizeof (dist)); for (int i = 1 ; i <= n; i ++) dist[i][i] = 0 ; for (int i = 1 ; i <= m; i ++){ int u, v, w; scanf ("%d %d %d" , &u, &v, &w); dist[u][v] = w; }
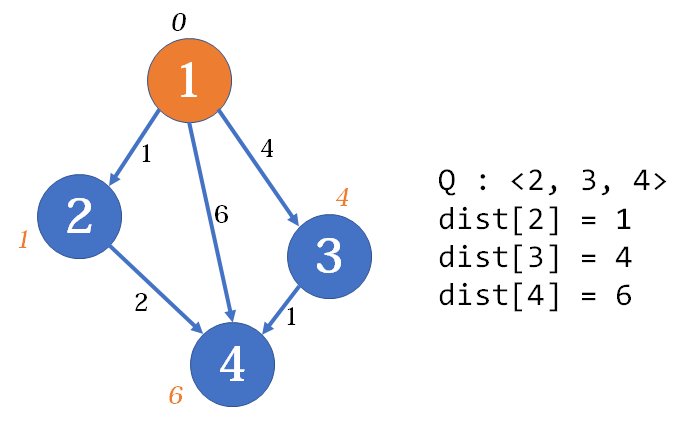
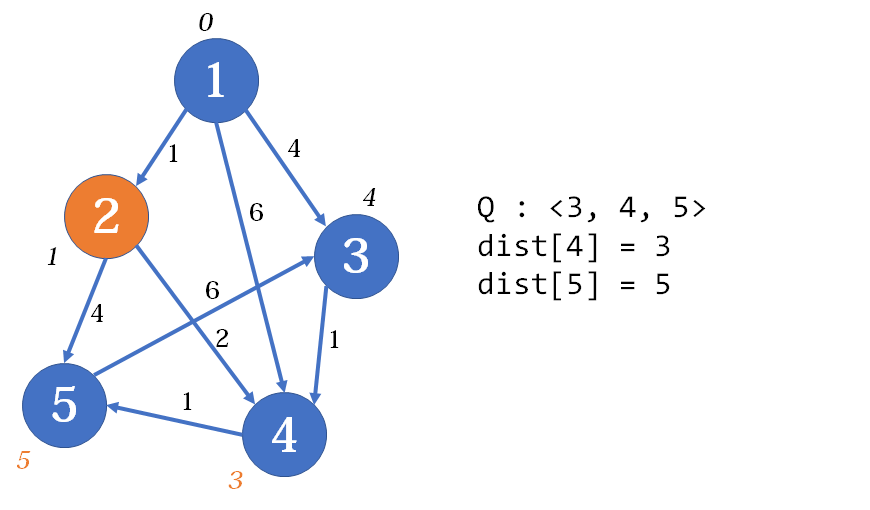
然后是第一趟,当中间点为
此时当中间点为
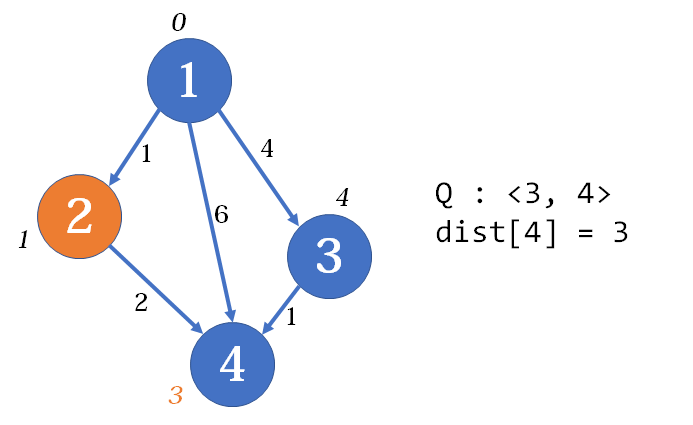
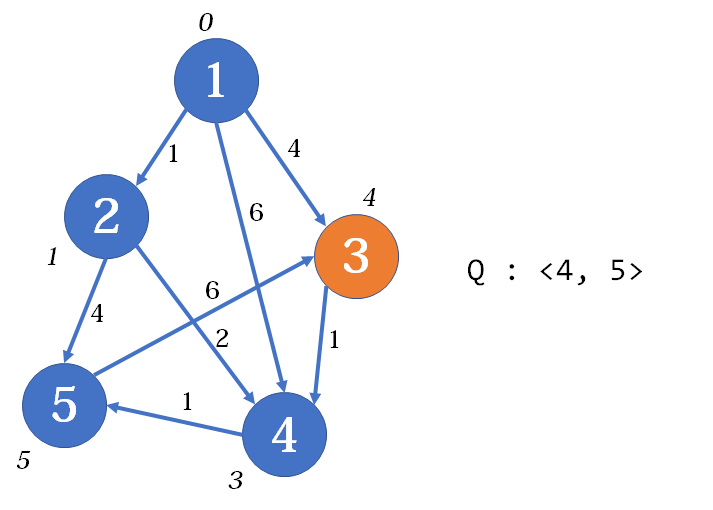
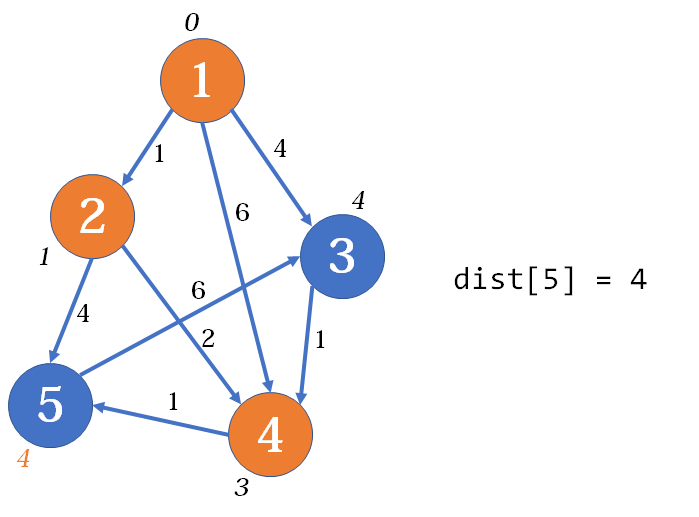
第二趟,中间点为
此时从
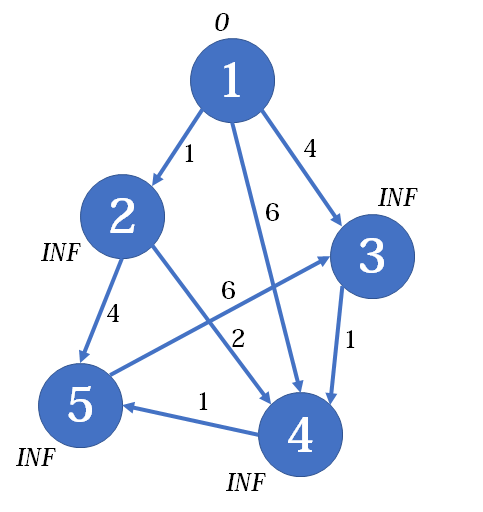
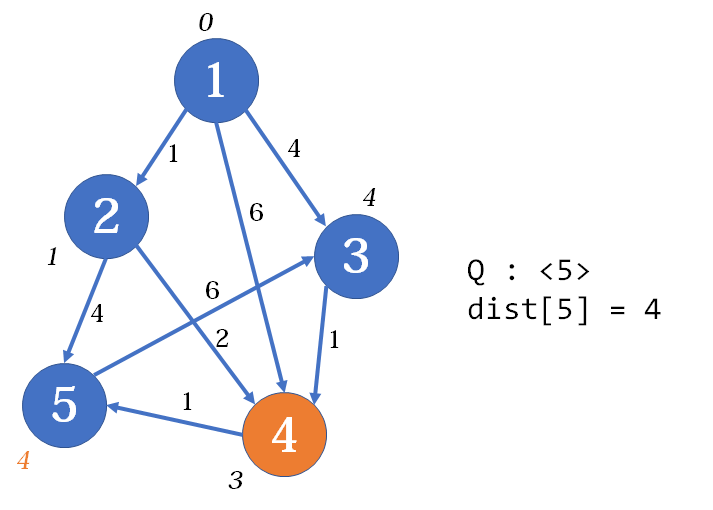
接下来是第三趟,当中间点为
虽然
时间复杂度是
Bellman-Ford 铃男 河流浅水处(无端翻译)
这里我们先来了解一个神奇的名词松弛 。
松弛操作 对边集合 当前 从起点
若存在
则更新
松弛 就是一种路径的更新(无非就是前面说的找中间商)
继续讲这个算法,因为起点被固定了,所以只需要一个一维数组
因为要找到最短路,所以我们要进行以下步骤:
1、松弛
2、再松弛 最短路的子路必然是最短路
3、再松弛
那么看到以上步骤,我直接暴力枚举。
要做的就是把所有边松弛
1 2 3 4 5 6 7 8 9 10 void Bellman_Ford (int n, int m) while (n - 1 --) { for (int i = 1 ; i <= m; i ++) { dist[edges[i].to] = min (dist[edge[i].to], dist[edge[i].from] + dist[edge[i].w]); } } }
来看一下过程:
这里可以直接暴力存边集 ,因为这个算法不关心能连到哪条边。
时间复杂度是
而且这个 负权环 的情况,只需再对所有边松弛一次,如果这次还有点被更新,就说明存在负权环。因为在正常情况下,最短路上的点是少于 莫名喜感?)
SPFA 关于
可以观察到
一开始,先把源点放入队列:
现在对于
现在队首是
后面的流程就不多说了,接下来看看有
流程与前面相同,到了
然后到达
接下来
接下来是
显然因为我们只更新这个点能到达的点 ,所以我们就省去了松弛其他无关紧要的边的时间,而且也不会松弛已经松弛过的边 ,目的只有得到从源点到终点的最短路 ,所以就快了很多(据说随机数据下期望时间复杂度是
总结一下,
只让当前点能到达的点入队
如果一个点已经入队,不重复入队
如果一条边还未更新到,它的终点肯定不入队
原理是,我们的目的是先松弛一个点和所有它的终点连接的边 ,将这些能到达的点加入队列,然后重复这个操作,如果有别的点能到达这个点,那说明这个前者肯定已经入过队了,那么利用三角形原理松弛这条边。
我们用一个
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 void SPFA (int s) queue <int > Q; Q.push (s); while (!q.empty ()) { int p = Q.front (); Q.pop (); inqueue[p] = 0 ; for (int i = head[p]; i; i = edge[i].nxt) { int to = edge[i].to; if (dist[to] > dist[p] + edge[i].w) { dist[to] = dist[p] + edge[i].w; if (!inqueue[to]) { inqueue[to] = 1 ; q.push (to); } } } } }
但是它的时间复杂度极不稳定 ,最坏情况下可能被卡成
判负权环 ,不过需要记录下每个点进入队列的次数,当一个点入队次数超过
Djikstra 这种算法,不妨叫它 (原因详见 nottttttthy的一篇题解 )
说点正经的,这是一个复杂度稳定 的算法。
贪心 的思想,现在假定一张没有负权 的图。首先,起点到起点的距离是 能直接到达的点 进行松弛。
因为没有负边,所以我们可以肯定,离起点最近的那个顶点的 ,为什么?显然因为不可能经由其他点,使该起点到该点的距离变得更远。
那现在来看
我们对 直接到达 或经由 到达每个点的最短距离。我们这时候取出未访问过的
继续这个操作,现在我们对
然后分别去看
总结一下, 离起点最近 而没有被访问过的 点,然后松弛所有它和它能到达的所有点。
如何取出这个点?如果暴力寻找,那就是朴素的 堆优化 。具体而言,就是使用一个优先队列 (或者手写堆)来维护所有节点。这样可以实现在
首先写一个结构体:
1 2 3 4 struct Polar { int dist, id; Polar (int dist, int id) : dist (dist), id (id) {} };
然后写一个仿函数(也可以重载
1 2 3 4 5 6 struct cmp { bool operator () (Polar a, Polar b) return a.dist > b.dist; } }; priority_queue <Polar, vector <Polar>, cmp> Q;
来看
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void Djikstra (int s) memset (dist, inf, sizeof (dist)); dist[0 ] = 0 ; Q.push (Polar (0 , s)); while (!Q.empty ()) { int p = Q.top ().id; Q.pop (); if (vis[p]) continue ; vis[p] = 1 ; for (int i = head[p]; i; i = edge[i].nxt) { int to = edge[i].to; dist[to] = min (dist[to], dist[p] + edge[i].w); if (!vis[to]) Q.push (Polar (dist[to], to)); } } }
显然,我们也可以用
1 2 typedef pair <int , int > Pair;priority_queue <Pair, vector <Pair>, greater<Pair> > Q;
这样的代码与之前只有三行的区别:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void Djikstra (int s) memset (dist, inf, sizeof (dist)); dist[s] = 0 ; Q.push (make_pair (0 , s)); while (!Q.empty ()) { int p = Q.top ().second; Q.pop (); if (vis[p]) continue ; vis[p] = 1 ; for (int i = head[p]; i; i = edge[i].nxt) { int to = edge[i].to; dist[to] = min (dist[to], dist[p] + edge[i].w); if (!vis[to]) Q.push (make_pair (dist[to], to)); } } }
路径打印 对于这种简单的任务,我们只需要一个数组
然后在最后输出一整坨路径就可以了(量词爆炸!)。
最短路树 这个东西感觉和最短路没啥关系但是因为看着像
用一道板子题来开始这个话题:
Shortcut G
每天晚上,
每块草地中有一些奶牛,如果它们发现有多条路径消耗时间一样少,它们会选择字典序较小的那一条。
要做的操作就是从节点 最短路树 ,然后跑
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 #include <bits/stdc++.h> #define int long long using namespace std ;const int N = 1e5 + 1 ;struct Edge { int nxt, to, w; } edge[N * 20 ]; struct Node { int id, val; bool operator < (Node x) const { return val > x.val; } }; int head[N], cnt;int n, m, t, c[N];int dist[N], siz[N], ans;bool vis[N], f[N];priority_queue <Node> Q; vector <int > G[N / 10 ];inline void add_edge (int u, int v, int w) edge[++ cnt].to = v; edge[cnt].w = w; edge[cnt].nxt = head[u]; head[u] = cnt; } void dijkstra (int s) Q.push ({1 , 0 }); while (!Q.empty ()) { Node p = Q.top (); Q.pop (); if (vis[p.id]) continue ; vis[p.id] = 1 ; dist[p.id] = p.val; for (int i = head[p.id]; i; i = edge[i].nxt) Q.push ({edge[i].to, p.val + edge[i].w}); } } void dfs (int p) siz[p] = c[p]; f[p] = 1 ; for (vector <int > :: iterator it = G[p].begin (); it != G[p].end (); it ++) if (!f[*it]) { dfs (*it); siz[p] += siz[*it]; } ans = max (ans, siz[p] * (dist[p] - t)); } signed main () int x, y, z; scanf ("%lld %lld %lld" , &n, &m, &t); for (int i = 1 ; i <= n; i ++) scanf ("%lld" , &c[i]); for (int i = 1 ; i <= m; i ++) { scanf ("%lld %lld %lld" , &x, &y, &z); add_edge (x, y, z); add_edge (y, x, z); } dijkstra (1 ); memset (vis, 0 , sizeof vis); for (int i = 1 ; i <= n; i ++) for (int j = head[i]; j; j = edge[j].nxt) if (dist[edge[j].to] == dist[i] + edge[j].w && !vis[edge[j].to]) { vis[edge[j].to] = 1 ; G[i].push_back (edge[j].to); G[edge[j].to].push_back (i); } dfs (1 ); printf ("%lld\n" , ans); }
Johnson 但是一出现就是巅峰。
因为数据会出现负环,会卡
任意两点之间的最短路可以通过跑
但是有负环。
那你可能就会想到给所有边加上一个更大的正数,可惜这已经不是最短路了,不然将绝杀。
而这里我们使用一个编号为
接下来用
假如存在一条从
这里先鸽了,暑假找个机会补起来。