不能抱有半吊子的心态，必须要有坚强的意志和信念。——《甘城光辉游乐园》

线段树

线段树（Segment Tree），一种用于维护区间信息的数据结构。与树状数组相比，它可以实现 的区间修改，还可以同时资瓷多种操作，更具有通用性。

线段树的概念

线段树是一棵平衡二叉树，母结点表示整个区间的和，越往下区间越小。线段树的每个结点对应一条线段（区间），但并不保证所有线段（区间）都是线段树的节点。

我是一棵线段树！

线段树的入门食用

每个 结点的子节点是 和 ，假如结点 储存 的和，设 ，那么两个子节点管理的区间就是 和 的和。

考虑使用递归在数组建树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void build (int l = 1, int r = n, int p = 1)
{
	if (l == r) // 区间两端合并，确定子节点
		tree[p] = a[l]; // 给这个子节点赋数组中的值
	else
	{
		int mid = (l + r) >> 1; // 位运算，与 /2 等价，分治思想
		build (l , mid, p << 1); // 向下递归
		build (mid + 1, r, p << 1 | 1); // 另一个子节点和另一个区域向下递归
		tree[p] = tree[p << 1] + tree[p << 1 + 1]; // 合并两个子节点的值得到它们的父节点值
		// 位运算，与*2等价，优化 
	}
    
	return ;
}

看上去线段树确实比树状数组码量大（详情请见我的另一篇博文《树状数组的养成方法》）

区间修改

在提到区间修改之前，我们要引入一个“懒惰标记”的概念。

懒惰标记

懒惰标记对于那些正好的线段树节点的区间，我们不再递归下去，而是给打上一个“懒惰标记”，等到将来要用到它的子区间时，再向下传递。

先来上一份区间修改的菜（有非常非常详细的解释）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void update (int cl, int cr, int p, int l, int r, int d) 
{
	if (cr < l || cl > r) // 与目标区间无交集
		return ;
	else if (cl >= l && cr <= r) // 被目标区间包含 
	{
		tree[p] += (cr - cl + 1) * d; // 值就是区间长度（多少个子节点）乘上给到的值了
		if (cr > cl) // 如果并非子节点，就打上懒惰标记
			lazy[p] += d; // 加值
	}
	else // 与目标区间有交集但不包含 
	{
		int mid = (l + r) >> 1; // 二分思想
		
		lazy[p << 1] += lazy[p]; // 此时用到这个区间，将懒惰标记向下传递给两个子节点 
		lazy[p << 1 | 1] += lazy[p];
		
		tree[p << 1] += (mid - cl + 1) * lazy[p]; // 修改节点对应区间
		tree[p << 1 | 1] += (cr - mid) * lazy[p]; // 这里本该是 (cr - (mid + 1) + 1)
		
		lazy[p] = 0; // 清除懒惰标记（不清掉会因为某些不可抗力而WA掉）
		
		update (cl, mid, p << 1, l, r, d); // 二分思想递归下去 
		update (mid + 1, cr, p << 1 | 1, l, r, d);
		
		tree[p] = tree[p << 1] + tree[p << 1 | 1]; // 递归回来了，由两个子区间获得父区间的值 
	}
}

过程模拟

这个过程的模拟（自己可以先来一遍试试）：

1、与目标区间无交集

第一种可能性，无交集

此时直接剪枝，退出递归。

1
2
if (cr < l || cl > r) // 与目标区间无交集
	return ; // 剪枝

2、被目标区间包含

第二种可能性，被包含

此时给 区间赋值，如果不是子节点就打上懒惰标记。

1
2
3
4
5
tree[p] += (cr - cl + 1) * d; 
/* 区间长度（有多少个子节点）乘上每个节点应该加上的值，
换句话说，就是你下面所有子节点该得到的，一次性丢给这个父节点了 */
if (cr > cl) // 如果并非子节点，就打上懒惰标记 
	lazy[p] += d;

3、与目标区间有交集但不被包含，此时采用分治思想

第三种可能性，有交集

此时二分查找区间，向两个子节点传递懒惰标记，修改对应区间，二分标准递归，得到父节点的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
if (cr > l && cl < r) // 此时区间条件，当然偷懒的话也可以写成 else 
{
	int mid = (l + r) >> 1; // 二分区间
		
	lazy[p << 1] += lazy[p]; // 将懒惰标记向下传递给两个子节点，而且记住是 += ，因为原来可能存在其他的标记
	lazy[p << 1 | 1] += lazy[p];
		
	tree[p << 1] += (mid - cl + 1) * lazy[p]; // 修改节点对应区间
	tree[p << 1 | 1] += (cr - mid) * lazy[p]; // 这里本该是 (cr - (mid + 1) + 1)
		
	lazy[p] = 0; // 清除懒惰标记
		
	update (cl, mid, p << 1, l, r, d); // 二分思想递归下去 
	update (mid + 1, cr, p << 1 | 1, l, r, d);
		
	tree[p] = tree[p << 1] + tree[p << 1 | 1]; // 由两个子区间获得父区间的值 
}

感觉这里的代码也是板子（擦汗）。

另外一提，我们通常把传递懒惰标记值的过程封装成一个函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
inline void push_down (int p, int len) // 传递函数
{
	lazy[p << 1] += lazy[p]; // 获得懒惰标记的值
	lazy[p << 1 | 1] += lazy[p];
  
	tree[p << 1] += lazy[p] * (len - len >> 1); // 分长度啦！！！
	tree[p << 1 | 1] += lazy[p] * (len >> 1);
   	/* 可以发现父节点代表的区间是平分这个懒惰标记的，然后因为
   	我们多给了左儿子一点，所以是 (len - len >> 1)，不能搞
   	错，因为可能出现奇数的情况的，不用担心，因为二分到最后肯定
   	会分到左端点等于右端点 */
	lazy[p] = 0; // 清除懒惰标记（不要忘记！）
}

然后在 函数里这么调用：

1
push_down (p, cr - cl + 1);  // 传入父节点编号和父节点代表区间的长度（不要担心，后面我们会分成两半的）

乘法的情况

规定乘法优先，然后我们记两种懒惰标记，乘法和加法，先给这个节点乘上乘法懒惰标记，再加上给到的加法懒惰标记（如还是看不懂，可以去线段树模板题解那边再加深理解）。

还有，不要忘记给父节点的乘法懒惰标记初始化为 ，加法懒惰标记初始化为 ， 不然你的成绩就会变成加法懒惰标记的值（威胁）。

1
2
3
4
tree[p << 1] += (tree[p << 1] * multag[p] + addtag[p] * (len1));
tree[p << 1 | 1] += (tree[p << 1 | 1] * multag[p] + addtag[p] * (len2));
// len1 和 len2 表示子节点代表的区间长度， multag 表示乘法懒惰标记， addtag 表示加法懒惰标记
// 当然这里也可以写一个结构体来记一个点的所有东西（值，长度，懒惰标记）

单点修改

单点修改便是使左端点等于右端点的时候停就可以了，然后向上合并值，话说如果只有单点修改和区间修改的话，为什么不用树状数组呢？

区间查询

既然已经有了区间修改的经验，直接上区间查询的板子了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
inline int query (int cl, int cr, int p, int l, int r)
{
	if (cr < l || cl > r) // 与目标区间无交集
		return ; // 剪枝
	else if (cl >= l && cr <= r)
		return tree[p]; // 访问的这个点刚好包含了查找区间，那就返回吧
	else
	{
		int mid = (cl + cr) >> 1; // 二分
		push_down (p, cr - cl + 1);
		return query (cl, mid, p << 1, l, r) + query (mid + 1, cr, p << 1 | 1, l, r);
		//返回 tree[p] ，也就是父节点的值 
	}
}

一样的二分，一样的传递，一样的合并信息。

线段树的进阶食用

动态开点

通常来说，一般线段树的空间是总区间长的 的常数倍，空间复杂度是 。当我们不需要用到所有子节点的时候，就可以使用到动态开点——不再一次性建好树，而是一边修改，一边查询一边建立。而相应的，不再使用 和 表示左右儿子，而是用两个数组 和 来记录左右儿子的编号。设总查询次数为 ，这样的时间复杂度是 。

比起普通线段树，动态开点线段树有一个优势，就是可以处理零或负数位置。此时求 不能用 ，而是 ，因为 时会退出递归。

因为缓存命中（ ）等原因，动态开点线段树写成结构体形式往往会快一点。

结构体

这个结构体里存入节点值，懒惰标记，左右儿子的编号：

1
2
3
4
struct Segment_Tree { // 动态开点结构体
	int val, lazy = 0; // 定义节点值，懒惰标记
	int ls, rs; // 定义左儿子和右儿子的编号
} tree[MAXN]; // 定义数组

传递函数

传递与普通线段树只有一点点区别，就是左右儿子记录的更改：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
inline void push_down (int p, int len)
// 传递函数，传入父节点编号和父节点对应的长度 
{
	if (!tree[p].ls) // 如果左儿子不存在 
		tree[p].ls = ++ cnt; // 创建新节点 
	if (!tree[p].rs) // 如果右儿子不存在 
		tree[p].rs = ++ cnt; // 创建新节点
	if (tree[p].tag) // 如果在父节点存在懒惰标记，就要向下传递 
	{
		upd (tree[p].ls, tree[p].lazy, len / 2); // 将懒惰标记传给左儿子，详情见 upd 函数 
		upd (tree[p].rs, tree[p].lazy, len - len / 2); // 将懒惰标记传给右儿子，详情见 upd 函数
		tree[p].lazy = 0; // 用完懒惰标记要清空 
	}
}

这里的区间长度 和 是为了减少误差，可能出现奇数区间长度。

区间修改

区间修改和前面的普通线段树应该没什么区别：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
inline void upd (int p, int d, int len) // 修改值
// 传入编号，要修改的值，区间长度 
{
	tree[p].val += d * len; // 这个父节点修改值
	tree[p].tag = d; // 给懒惰标记赋值
}
inline void update (int l, int r, int d, int p = 1, int cl = L, int cr = R)
// 区间修改，传入目标区间端点，值，编号和当前查找区间 
{
	if (cl >= l && cr <= r) // 如果当前查找区间被目标区间包含
		return upd (p, d, cr - cl + 1); // 传入编号，值和区间长度
	push_down (p, cr - cl + 1); // 向下传递懒惰标记
	int mid = (cl + cr - 1) / 2; // 算出当前查找区间的中点
	if (mid >= l) // 如果中点大于目标左端点，说明左边区间被包含 
		update (l, r, d, tree[p].ls, cl, mid); // 传入左儿子和左区间向下递归 
	if (mid < r) // 如果中点小于目标右端点，说明右边区间被包含 
		update (l, r, d, tree[p].rs, mid + 1, cr); // 传入有儿子和右区间向下递归 
	tree[p].val = tree[tree[p].ls].val + tree[tree[p].rs].val; // 向上返回给父节点值
	
	return ; 
}

来看一下这段代码：

1
2
3
4
if (mid >= l) // 如果中点大于目标左端点，说明左边区间被包含 
	update (l, r, d, tree[p].ls, cl, mid); // 传入左儿子和左区间向下递归 
if (mid < r) // 如果中点小于目标右端点，说明右边区间被包含 
	update (l, r, d, tree[p].rs, mid + 1, cr); // 传入有儿子和右区间向下递归

如果不理解，可以模拟一下分区间的过程：

当前查找区间的中点大于目标区间左端点

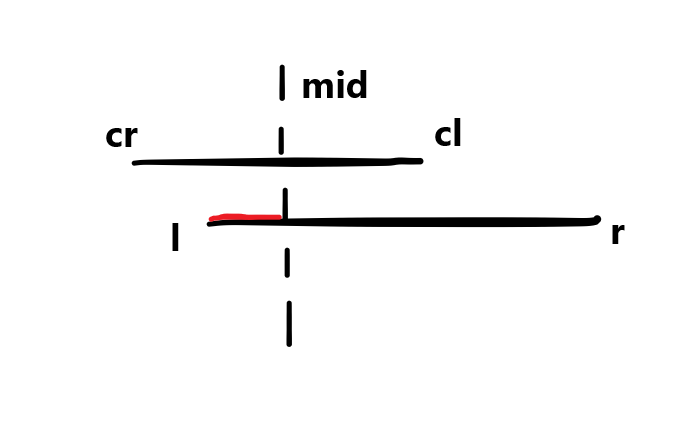
看到左边还有一坨被包含

1
2
if (mid >= l) // 如果中点大于等于目标左端点，说明左边区间被包含 
		update (l, r, d, tree[p].ls, cl, mid); // 传入左儿子和左区间向下递归

当前查找区间的中点小于目标区间右端点

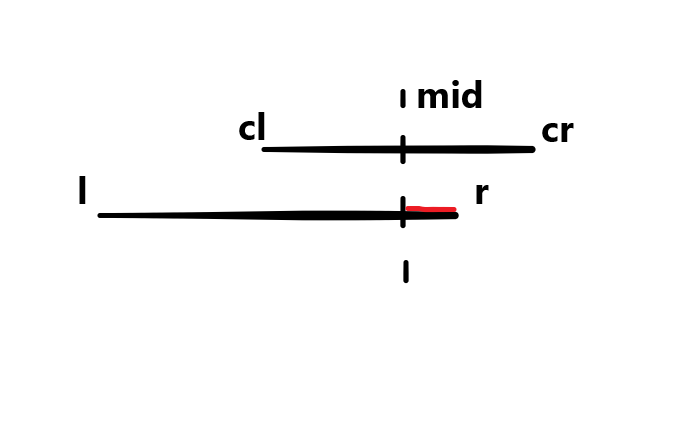
看见右边有一坨被包含

1
2
if (mid < r) // 如果中点小于目标右端点，说明右边区间被包含 
		update (l, r, d, tree[p].rs, mid + 1, cr); // 传入有儿子和右区间向下递归

如果要问为什么一个是小于号，一个是大于等于号的话，应该是因为左区间往往较长。

查询函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
inline int query (int l, int r, int p = 1, int cl = L, int cr = R)
// 区间查询，传入目标区间，初始编号，传入当前查找区间 
{
	if (cl >= l && cr <= r) // 当前查找区间被目标区间包含 
		return tree[p].val; // 返回节点值
	push_down (p, cr - cl + 1); // 传入父节点编号和父节点对应长度
	int mid = (cl + cr - 1) / 2; // 算中间点 
	if (mid >= r) // 当前查找区间中点大于右端点 
		return query (l, r, tree[p].ls, cl, mid); // 返回左区间 
	if (mid < l) // 当前查找区间中点小于左端点
		return query (l, r, tree[p].rs, mid + 1, cr); // 返回右区间 
	else
		return query (l, r, tree[p].ls, cl, mid) + query (l, r, tree[p].rs, mid + 1, cr); // 返回整一段区间 
}

再来看一下区间判断：

1
2
3
4
5
6
if (mid >= r) // 当前查找区间中点大于右端点 
	return query (l, r, tree[p].ls, cl, mid); // 返回左区间 
if (mid < l) // 当前查找区间中点小于左端点
	return query (l, r, tree[p].rs, mid + 1, cr); // 返回右区间 
else
	return query (l, r, tree[p].ls, cl, mid) + query (l, r, tree[p].rs, mid + 1, cr); // 返回整一段区间

当前查找区间中点大于目标区间右端点

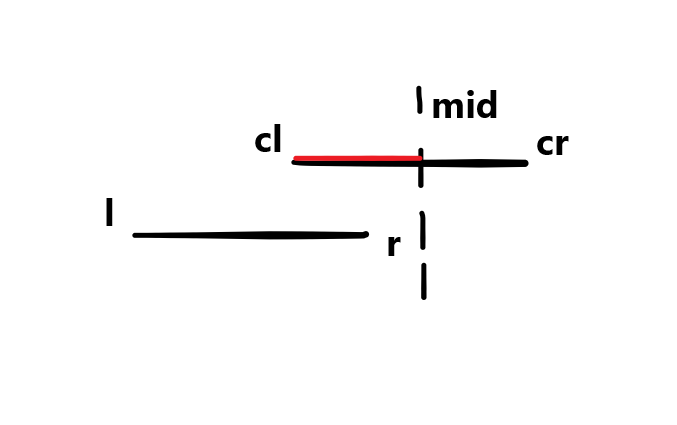
果断放弃右边

1
2
if (mid >= r) // 当前查找区间中点大于右端点 
	return query (l, r, tree[p].ls, cl, mid); // 返回左区间

当前查找区间中点小于目标区间左端点

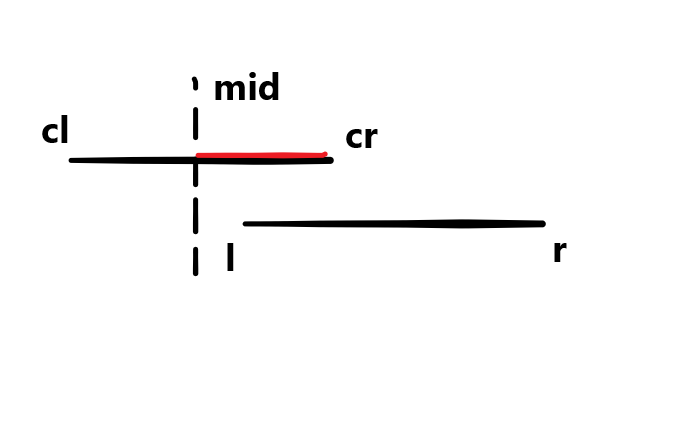
果断放弃左边

1
2
if (mid < l) // 当前查找区间中点小于左端点
	return query (l, r, tree[p].rs, mid + 1, cr); // 返回右区间

当前查找区间的左边和右边都被包含

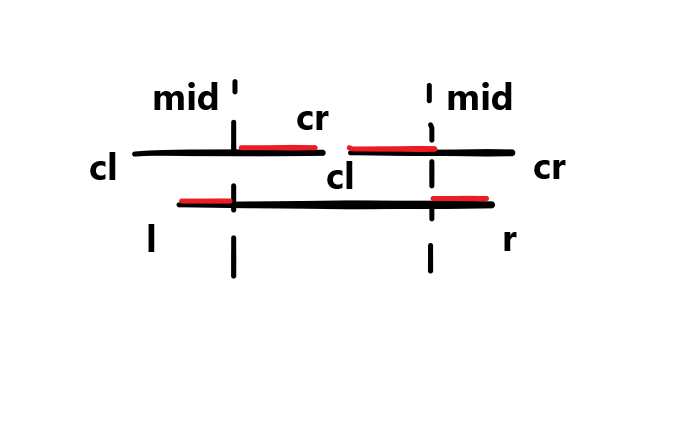
一个都不能落下！

1
2
else
	return query (l, r, tree[p].ls, cl, mid) + query (l, r, tree[p].rs, mid + 1, cr); // 返回整一段区间,这里维护的是和，可以改成别的

可以看到，除了在 传递函数里进行了新节点的创建，其他基本与普通线段一致。动态开点线段树不需要 ，通常用在没有给初始数据的场合（比如初始全 ），这时更能表现出优势。

当然，除了动态开点，先离散化再建树也可以达到效果。但动态开点写出来更简单直观，而且在强制在线时只能这样做。

权值线段树

桶我们经常使用。而权值线段树就是用线段树维护一个桶，每个叶节点的权值存的是代表的值出现的次数。它可以 （ 是值域）地查询某个范围内数出现的总次数。不仅如此，它还可以 地求得第 大的数。事实上，它常常可以代替平衡树使用。

由于权值线段树需要按值域开空间，所以常常使用到动态开点。

对于这个数组：

我们可以画出这样一张图：

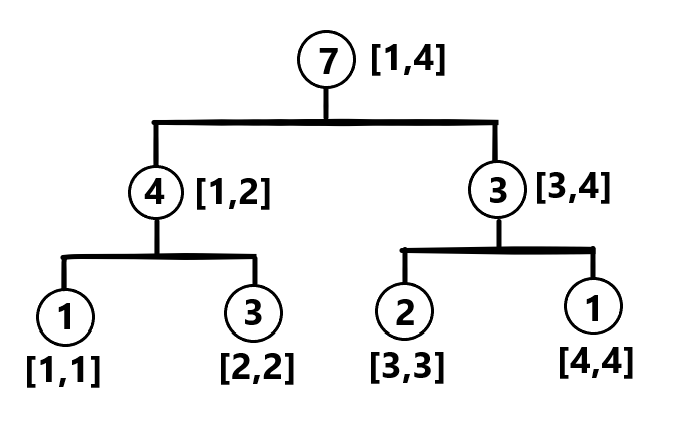
我是权值线段树！

单点修改

单点修改基本与普通线段树一致：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
inline void upd (int p, int d, int len) // 修改值，传入编号，值和个数
{
	tree[p].val += d * len;
}
inline void update (int x, int d, int p = 1, int cl = L, int cr = R)
// 单点修改，传入位置（代表值），个数，节点编号，当前查找区间，区间端点存的是数字
{
	if (cl == cr) // 如果是叶节点 
		return upd (p, d, 1); // 这里传入编号，值和长度为一
	push_down (p); // 如果不是叶节点，就向下创造子节点
	int mid = (cl + cr - 1) >> 1; // 当前查找区间的中点 
	if (x <= mid) // 如果要填入的数小于等于当前区间中点的值 
		update (x, d, tree[p].ls, cl, mid); // 向左边找位置 
	else // 如果填入的数大于当前区间中点的值 
		update (x, d, tree[p].rs, mid + 1, cr); // 向右边找位置
	tree[p].val = tree[tree[p].ls].val + tree[tree[p].rs].val; // 返回这个区间的个数 
}

然后在增加或减少一个数字的次数时，这样调用函数：

1
2
3
4
5
6
7
8
inline void insert (int x) // 传入要增加的数字 
{
	update (x, 1); // 选定目标点（数字） ，给它加一 
}
inline void remove (int x) // 传入要减少的数字
{
	update (x, -1); // 选定目标点（数字），给它减一 
}

传递函数

权值线段树只会用到单点修改，所以减少了往下丢懒惰标记的操作：

1
2
3
4
5
6
7
inline void push_down (int p) // 创造子节点函数，传入编号 
{
	if (!tree[p].ls) // 如果左儿子不存在 
		tree[p].ls = ++ cnt; // 增加新节点 
	if (!tree[p].rs) // 如果右儿子不存在 
		tree[p].rs = ++ cnt; // 增加新节点 
}

查询第 k 大数字

当左子树内权值大于等于剩余查询次数（可以看成是查掉了多少个元素）时，则递归进入左子树进行查询，否则递归进入右子树进行查询，并减去左子树权值：

1
2
3
4
5
6
7
8
9
10
11
inline int query_kth (int k, int p = 1, int cl = L, int cr = R)
// 查询第k大元素（不是数，是元素），传入排名，和初始数据
{
	if (cl == cr) // 如果搜到叶节点
		return cl; // 返回代表的数字
	int mid = (cl + cr - 1) >> 1;
	if (tree[tree[p].ls].val >= k) // 左子树权值大于当前剩余查询次数
		return query_kth (k, tree[p].ls, cl, mid); // 向左子树进入递归查找 
	else // 当前剩余查询次数比左子树权值大 
		return query_kth (k - tree[tree[p].rs].val, mid + 1, cr); // 向右子树进行递归查找 
}

利用二分思想，当左子树权值大于当前剩余查询次数时，就说明当前要找的数在左区间；当左子树权值小于当前查询次数时，说明前面的个数还不够，要去右边查找，我们可以来模拟一下。

使用上面的图，假设我们现在要找到第 大的数。

第一步，我们先看左子树和右子树的权值，显然选择向右走：

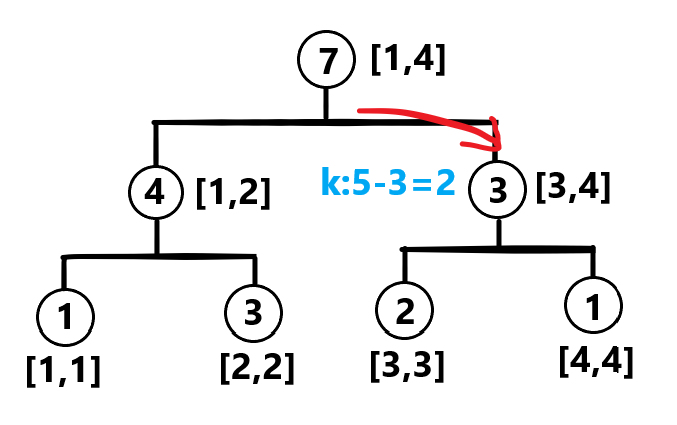
直接选择右边

此时查询次数剩下 次，下一次操作我们选择左子树，这里的数据太水了，直接找到了：

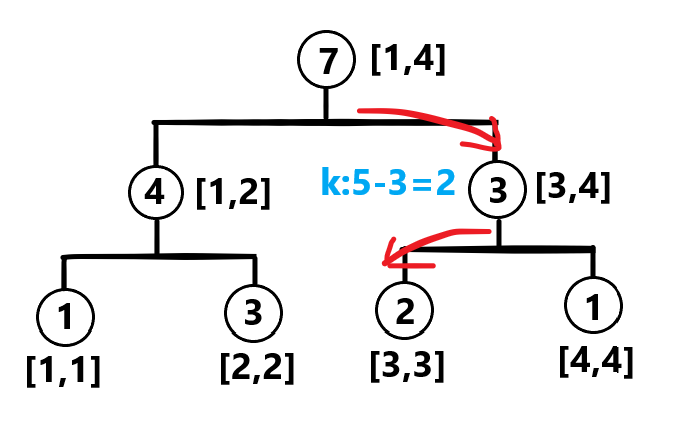
这次选择左边，次数用完了

操作原理就是这个每次比较每个小区间内元素的个数，选择左边或右边，至于为什么选择左区间时不用减去查询次数（区间内元素个数），是因为每次进入一个父区间时，我们把左区间看做父区间前 个数，如果 都不到这个数，就不用减去（减去都成负数了）。

查询 x 的排名

只需要查询线段树 权值的区间和再加一就彳亍了，换句话说，就是查在 在前有多少个元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
inline int query (int l, int r, int p, int cl, int cr) // 查询函数 
{
	if (cl >= l && cr <= r) // 当前查找区间被目标区间包含 
		return tree[p].val; // 返回区间元素个数
	push_down (p); // 向下使用子节点
	int mid = (cl + cr - 1) >> 1; // 求当前查找区间中点
	if (mid >= r) // 中点在右端点右边，解释可以去上面看 
		return query (l, r, tree[p].ls, cl, mid); // 向左区间递归 
	if (mid < l) // 中点在左端点左边 
		return query (l, r, tree[p].rs, mid + 1, cr); // 向右区间递归 
	else // 当前查找区间的左右半边都有被包含 
		return query (l, r, tree[p].ls, cl, mid) + query (l, r, tree[p].rs, mid + 1, cr); // 同时向下递归 
}
int countl (int x) // 算 x 前有多少个元素 
{
	return query (L, x - 1, 1, L, R); // 传入左端点和这个点的前面那个点 
}
int rank (int x) // 查询 x 的排名 
{
	return countl (x) + 1; // 返回左边有多少个元素 + 1 
}

查询前驱

意思就是求 前面那个数。

1
2
3
4
5
inline int pre (int x) // 查询前驱 
{
	int r = countl (x); // 求出前面有多少个元素
	return query_kth (r); // 返回前面那个数（因为是前面的第 r 个数） 
}

查询后继

意思就是求 后面的那个数

1
2
3
4
5
6
7
8
9
10
inline int countg (int x) // 查询 x 后面共有多少个元素 
{
	return query (x + 1, R); // 算后面有多少个元素 
}
inline int suc (int x) // 查询后继
{
	int r = tree[1].val - countg (x) + 1;
	// tree[1] 是根节点，权值代表共有多少个元素，减去 x 后面元素的个数再加一得到长度（从左端点到这个点） 
	return query_kth (r); // 排名第 r 个数是谁 
}

线段树的高级食用

线段树合并

现在假设我们有两棵被边缘偷吃过的权值线段树：

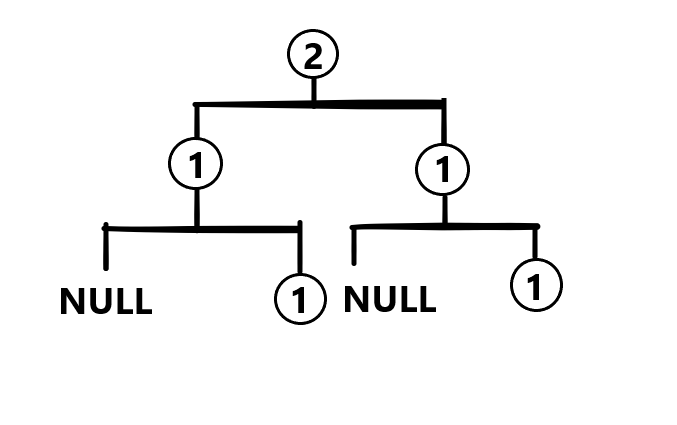
第一棵被边缘偷吃过的权值线段树

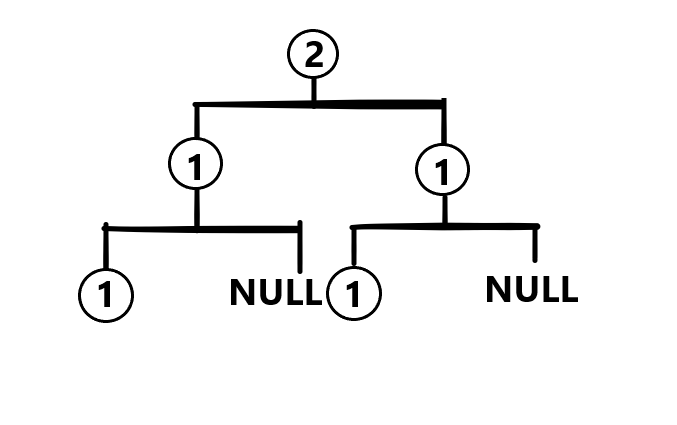
第二棵被边缘偷吃过的权值线段树

现在我们想要将这两棵线段树合并，最终结果会是这样的：

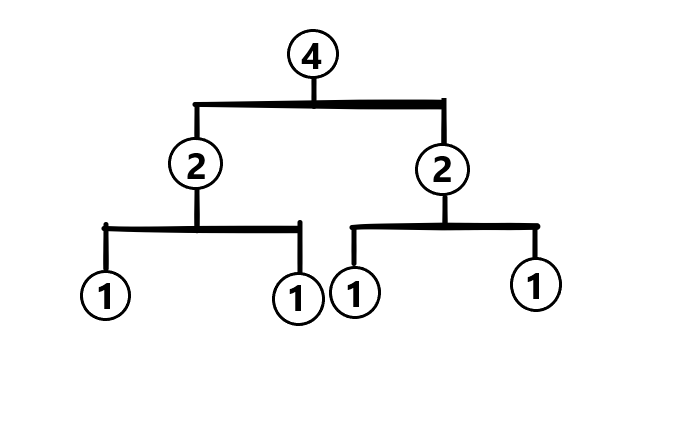
合并后得到的权值线段树

画的好丑（捂脸）。

说回正题，可以看出线段树合并，就是建立一棵新的线段树而且还保存了原有的两棵线段树的信息。最坏的时间复杂度是 。

过程很简单明了，如果第一棵树有一个 位置，但是第二棵树没有，那么新的线段树 位置就赋成第一棵树的 的权值 ，返回。

相反的，如果第二棵树有一个 位置，但是第一棵数没有，那么新的线段树 位置就赋成第二棵树的 的权值，返回。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
int merge (int a, int b, int cl, int cr) // 线段树合并  
{
	if (!a) return b; // 如果 a 没有，就用 b 的 
	if (!b) return a; // 如果 b 没有，就用 a 的 
	if (l == r)
		return a; // 按照所需合并  
	int mid = cl + cr >> 1;
	tree[a].ls = merge (tree[a].ls, tree[b].ls, l, mid); // 向左区间递归  
	tree[a].rs = merge (tree[a].rs, tree[b].rs, mid + 1, r); // 向右区间递归  
	push_up (a);
	return a;
}