以我的最弱，击败你的最强。——《落第骑士英雄谭》

并查集

并查集的概念

并查集（Union-find Disjoint Sets）是一种简洁而又不失优雅的数据结构之一，主要用于解决一些元素分组的问题。它管理一系列不相交的集合，并支持两种操作：

1、合并（ ） ：把两个不相交的集合合并为一个集合

2、查找（ ） ：查询两个元素是否在同一个集合内

这就好像一个家族问题，查询两个人是否有血缘关系（还好不是问我各个亲戚之间该叫什么，我可记不住这类乱七八糟的东西，每年探望亲戚前还要问一遍我妈 www ）

这类问题只要建立模型，把所有元素划分到若干个不相交的集合里，使用并查集进行维护就可以了。

并查集的引入

并查集的重要思想就是，用集合里的一个元素来代表这个集合，我们将这个点称为父节点，现在我们来看一下并查集的过程。

刚开始，所有元素都互不相交，所以它们各自构成了一个集合，所有集合的父节点都是自己，它们互是自己的大哥：

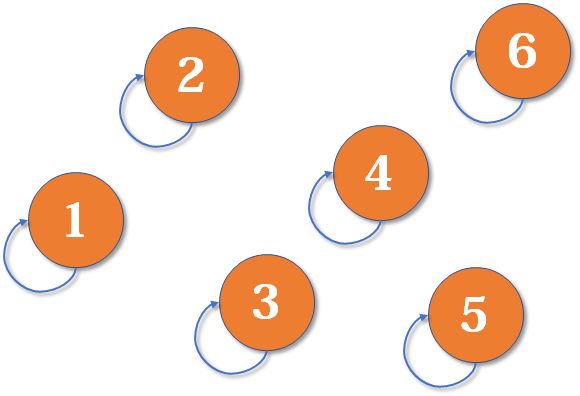
所有人都是自己的集合

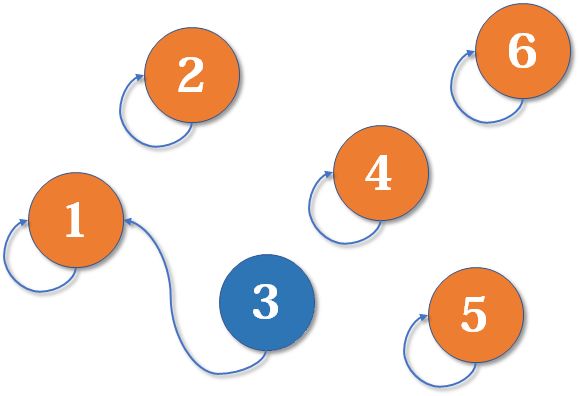
现在假设 号元素和 号元素打架， 号打输了，那么现在 号元素就是 号元素的父节点：

3号认1号为大哥

现在 号和 号打架， 号就成为 号的父节点：

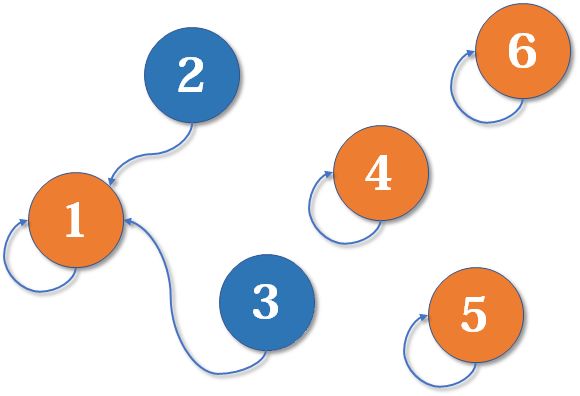
2号败给3号，但是成为1号的子节点

接下来假设 号也发生了刚刚的情况，现在情况变成这样：

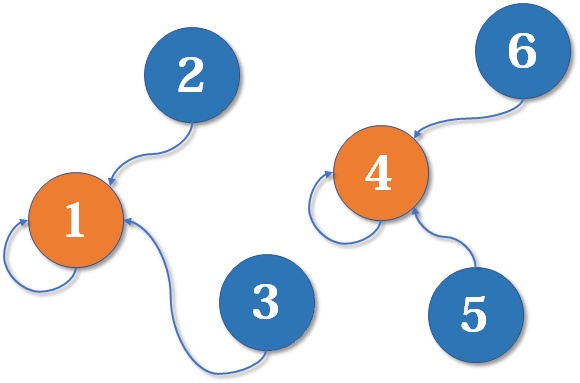
1号和4号代表了两个集合

最后，假设现在 号的小弟 号又和 号打架，输了，那 号就成为 号的子节点：

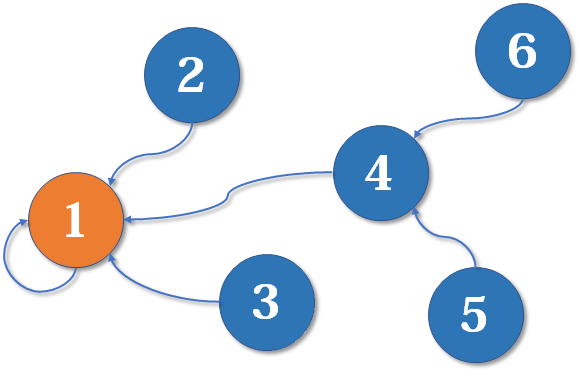
1号成为了所有人的大哥！

结束了，如果你仔细观察，就会发现这是一个树状结构，要寻找集合的代表元素，就要一层一层向上寻找父节点（图中自己指着自己的点）。根节点的父亲是它自己，我们可以直接把这张图画成一棵树：

“人”形结构

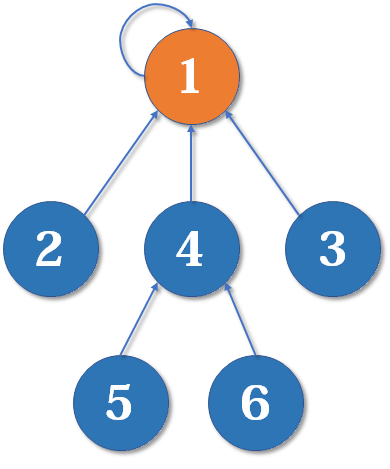
用这种方法，我们可以实现最简单的并查集。

并查集的食用

初始化

还记得我们说的吗，刚开始，每个元素都是自己的父节点。所以我们用一个数组 来记录每个元素的父节点是谁，因为每个元素有且只有一个父节点，所以这是可行的。

1
2
3
4
5
6
7
8
int fa[maxn];
void init () // 初始化 
{
	for (int i = 1; i <= n; i ++) // 遍历所有的点 
		fa[i] = i; // 每个点都是自己的父亲 
	
	return ;
}

查询

查询的过程就是在集合这棵树上找自己的根节点，我们使用递归的方法来一层一层向上寻找父节点，直至根节点（这个集合的代表）。如果要判断两个元素是否在同一个集合内，只要询问它们的根节点是否相同就可以了。

1
2
3
4
5
6
7
inline int find (int x) // 查询
{
	if (fa[x] == x) // 如果这个点的父节点是自己，也就是根节点 
		return x; // 返回根节点的编号 
	else
		return find (fa[x]); // 用当前这个点的父节点当做下一次递归的子节点 
}

当然我们也可以使用三目运算符将其合成为一句话。

1
2
3
4
inline int find (int x) // 查询
{
	return fa[x] == x ? x : find (fa[x]);
}

合并

合并操作就是先找到两个点的根节点然后将其合并，前者是后者的父节点或者后者是前者的父节点都没有关系，后面我们会讲到一个更合理的合并方法。

1
2
3
4
5
inline void merge (int x, int y) // 合并 
{
	int fx = find (x), fy = find (y); // 找到这两个点的父节点 
	fa[fx] = fy; // 这里可以调换 
}

路径压缩

最简单的并查集效率是比较低的，先来看一个场景：

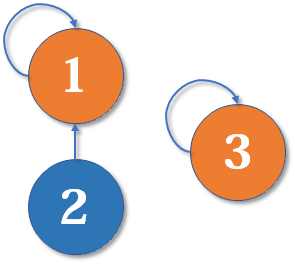
3号点是目前的独孤大侠

现在我们要 ，于是从 号点找到 号点， ：

排排排队，一起走

然后我们找到了 号点， 号点说如果自己做大哥，它就过来，于是我们执行 ：

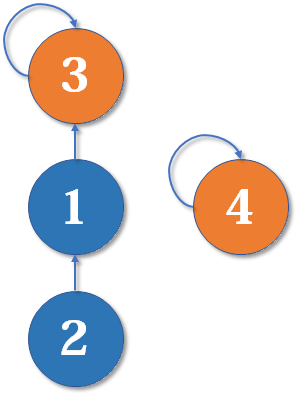
老鹰捉小鸡

从 号点找到 号点，从 号点找到 号点， ，然后就变成了这样：

排排排排队，一起走

这样就变成了一条链，显然随着链的长度的增加，想要从子节点找到根部的难度也变大了。

所以这里使用到路径压缩。既然我们只关心一个元素对应的根节点，那么我们希望步数尽量少，最好只有一步（贪到家了啊喂！！！），就像这样：

一步到胃

实现方法很简单，只要我们在查询的途中，把沿途的每个节点的父节点都设为根节点即可（从间接管辖变到了直接管辖）。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
inline int find (int x) // 查询 
{
	if (fa[x] == x) // 如果这个点的父节点是自己，也就是根节点
		return x; // 直接返回这个点的编号 
	else
	{
		fa[x] = find (fa[x]); 
		/* find 不断向上循环，注意左边的 fa[x]是最后的根节点，
		也就是用每次的父节点进行查询，一次性向上得到的父节点（前者）就是根节点*/ 
		return fa[x]; // 返回这个根节点
	}
}

当然通常简写成一行（压行大师）：

1
2
3
4
inline int find (int x) // 查询 
{
	return fa[x] == x ? x : (fa[x] = find (fa[x])); // 道理同上 
}

注意赋值运算符的优先级没有三目运算符高，要加括号。

按秩合并

注意，路径压缩后不等于并查集是菊花图（只有两层的图的俗称），而且只有路径压缩只在查询时进行，也只压缩一条路径，所以并查集的结构最终还是很复杂的，如下图，我们现在有一棵较复杂的树要和一个单元素的集合合并：

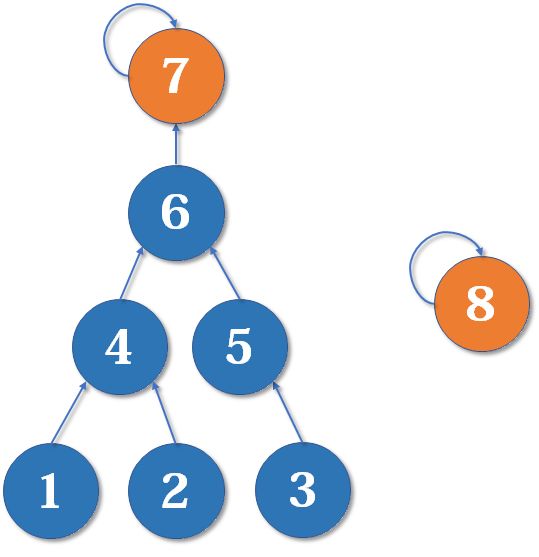
显然非常复杂

此时是把 号点作为 号点作为父节点好，还是 号点把 号点当做子节点好呢？

当然都不是！（大雾，难道不是把 号点的父节点设为 号点吗，请好好看一下我上面两个选择的逻辑关系）

来看一下两种情况：

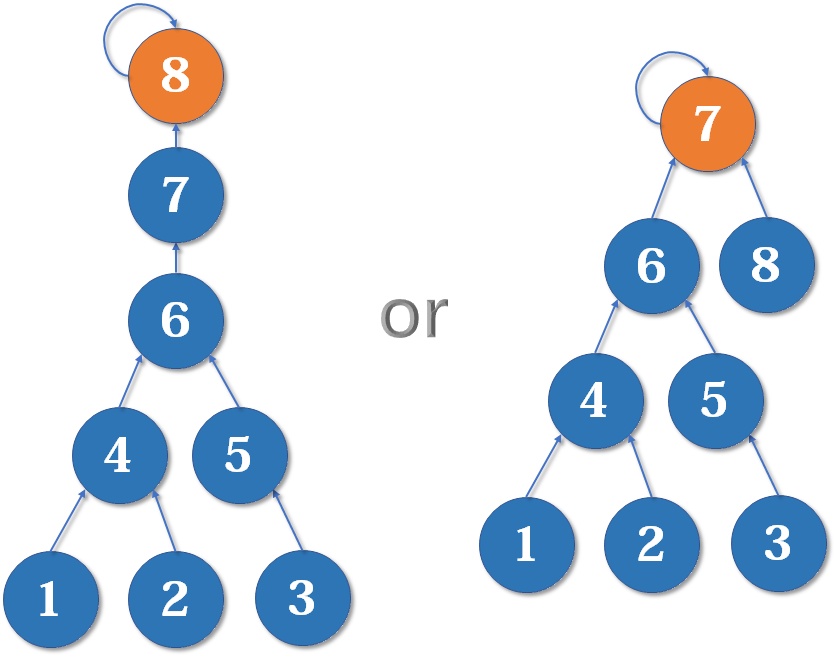
少年你的选择是什么

如果是第一种情况，会导致树的深度（树中最长链）增长，会增加时间；但是第二种情况的 号点不影响到其他无关点，所以更优。

所以我们应该把简单的树合并到复杂的树上，这样可以适当减少到根节点距离长的点的个数。

实现方法就是用一个数组 记录每个根节点对应的树的深度（如果不是根节点，其 相当于以它作为根节点的子树的深度），一开始把所以节点的（ ）秩设为 ，合并时比较这两个点的根节点的 ， 把 较小者往较大者上合并。

路径合并如果和按秩合并一起使用，时间复杂度接近 ，但是可能会破坏 的准确性。

初始化

1
2
3
4
5
6
7
8
9
10
void init ()
{
	for (int i = 1; i <= n; i ++) // 遍历所有点
	{
		fa[i] = i; // 自己设为自己的父节点
		rank[i] = 1; // 初始化为 1
	}
	
	return ;
}

合并

1
2
3
4
5
6
7
8
9
10
inline void merge (int x, int y)
{
	int fx = find (x), fy = find (y); // 获取父节点
	if (rank[fx] <= rank[fy]) // 将 rank 较小树合并到较大树上 
		fa[fx] = fy;
	else 
		fa[fy] = fx; // 反着来 
	if (rank[fx] == rank[fy] && fx != fy) // 如果两者的 rank 相等，且父节点本不同 
		rank[fy] ++; // 大树深度加一 
}

试问，为什么当深度相同的时候，新的根节点深度要加一？

假设现在我们有两棵深度为 的树，现在要合并 号点和 号点：

来模拟！！！

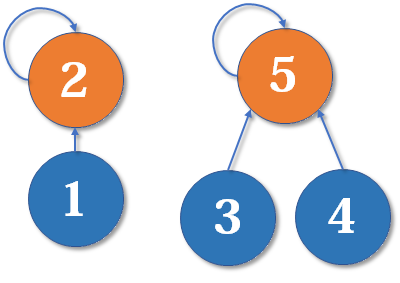
这里把 号点的父节点设为 号点（其实没有什么区别）

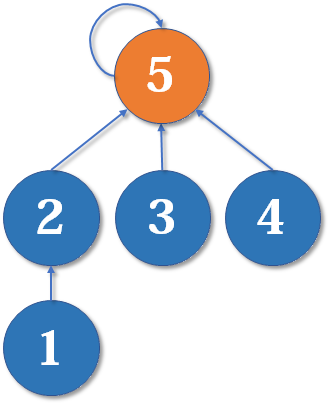
看到没有~看到没有~

显然这棵树的深度加一，另一种合并方式同样会使深度加一。