时间会冲淡痛苦的回忆,只有美好的事情才会永存。——《前进吧!登山少女》
树链剖分
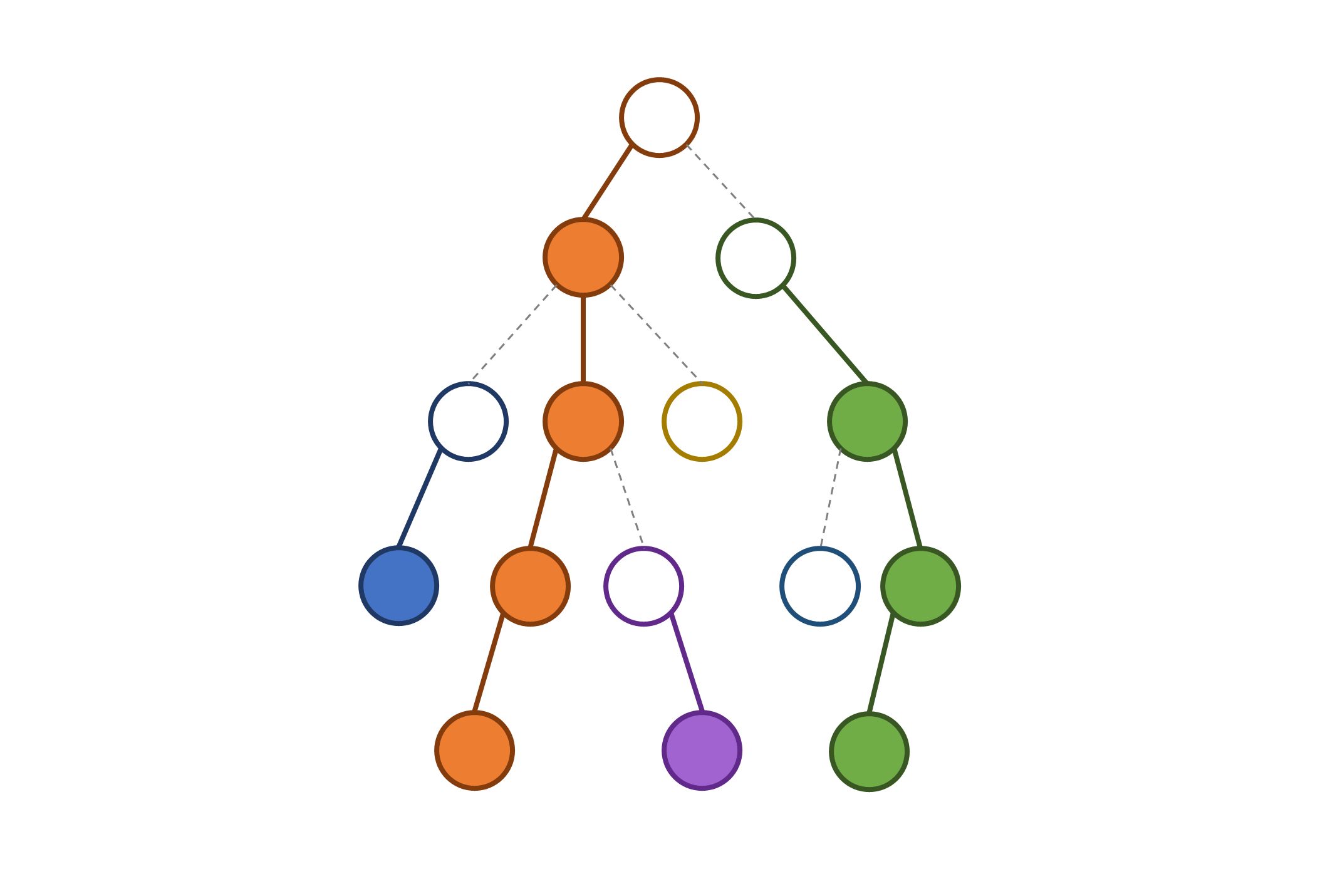
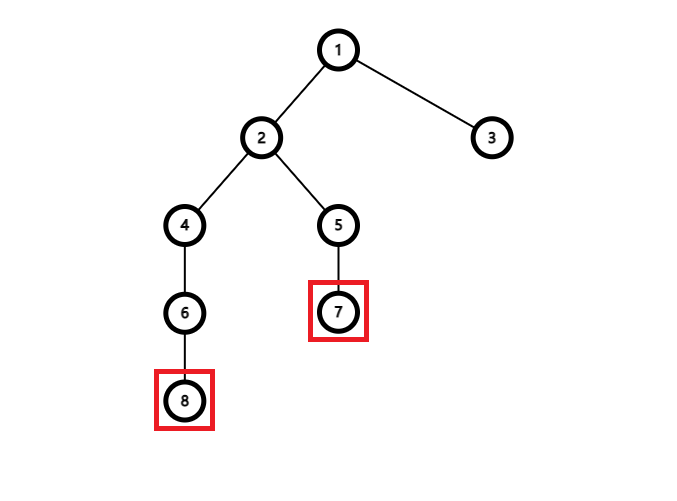
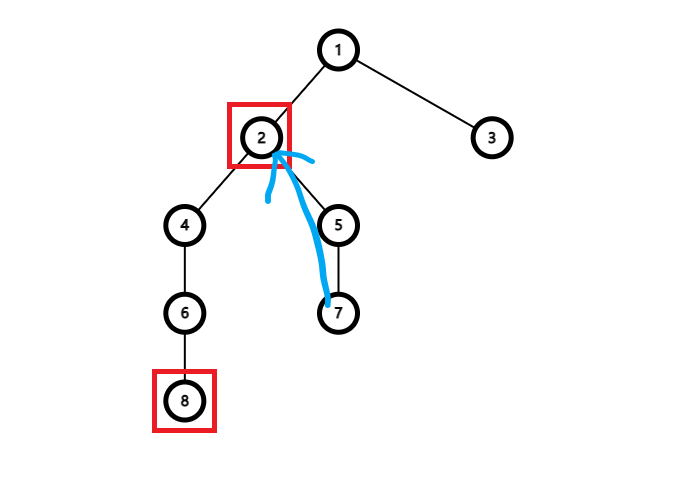
你看这个树它像不像一座山一样
你能不能换个题目,这个题目太阴间了。——龙潜月十五
树链剖分 是把一棵树分割成若干条链,以便于维护信息的一种方法,其中最常用的是轻重链剖分(Heavy - Light Path Decomposition) ,如果平时没有特别说明,树链剖分一般都指重链剖分。
重链剖分
定义 重子节点: 其子节点中子树最大的子节点 ,如果有多个子树最大的子节点,取其一,如果没有子节点,就无重子节点。
轻子节点: 只要不是重子节点,就是轻子节点。
重边: 一个节点连向其重子节点的边。
轻边: 一个节点连向其轻子节点的边。
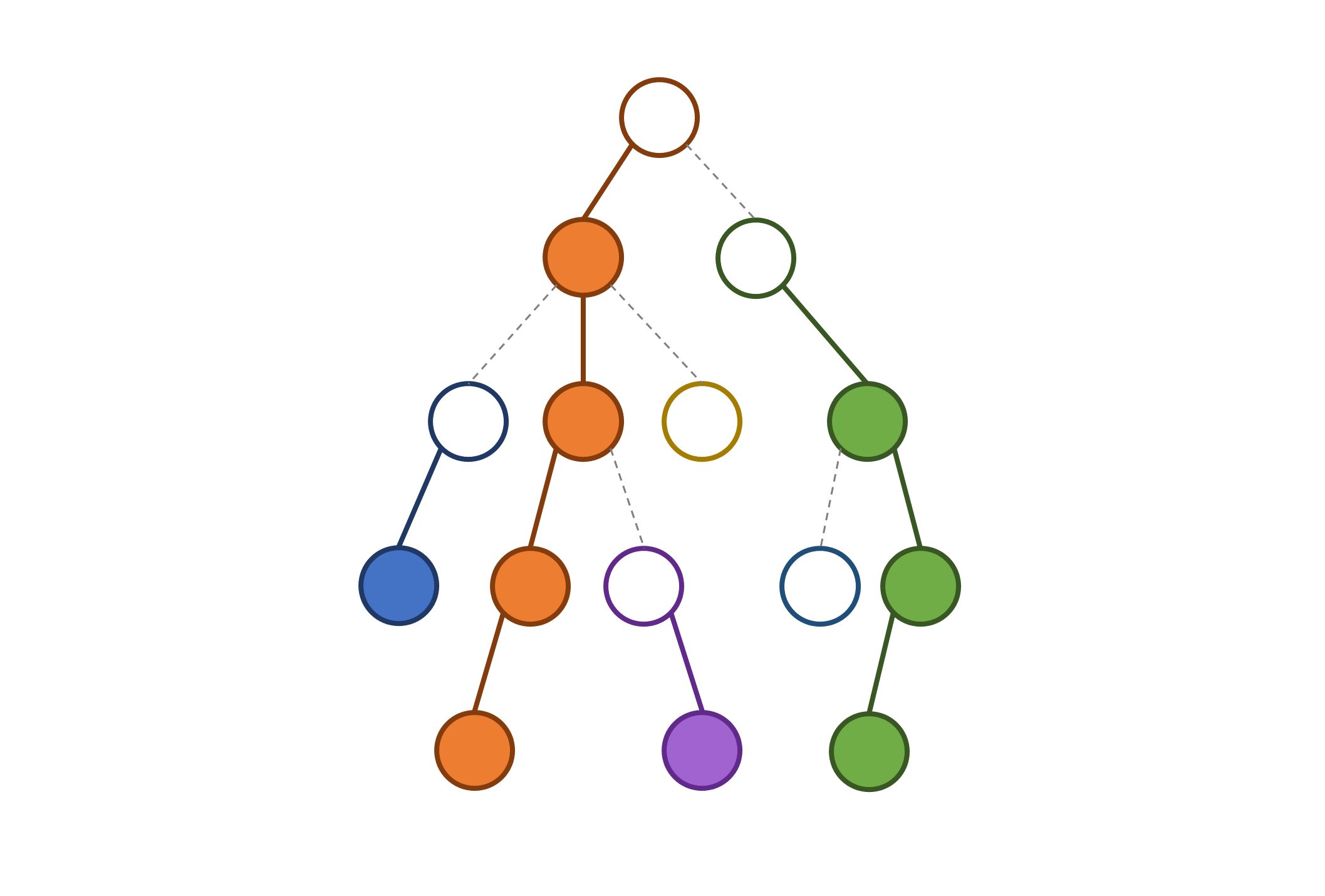
如果把根节点看做轻的,那么从每个轻节点出发,不断向下走重边,都对应了一条链,于是我们把树剖分成了
重链剖分有一个重要的性质,对于节点数为
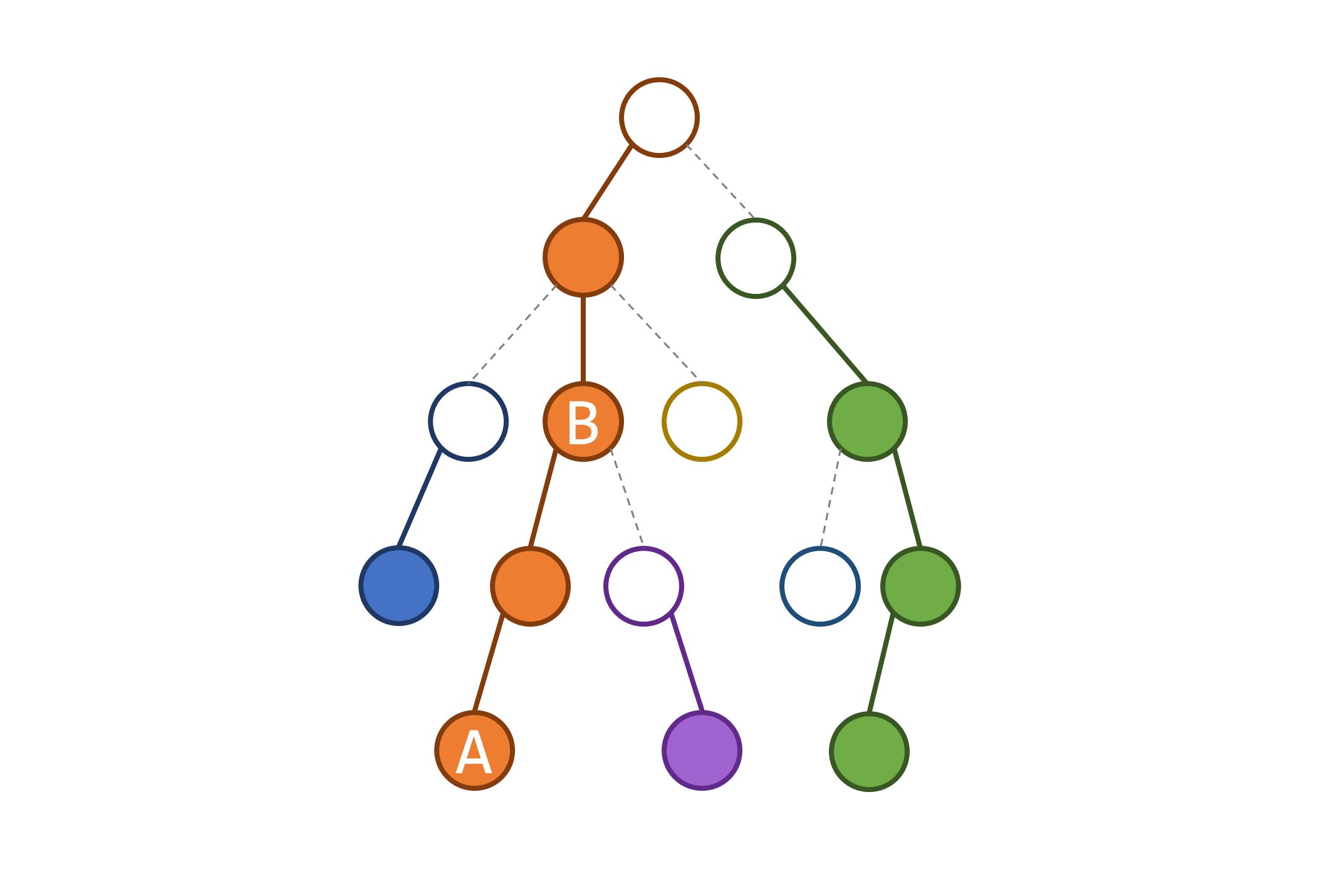
重链剖分的食用 基本剖分 我们通过两次 父节点 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 void dfs1 (int p, int d) int size = 1 , ma = 0 ; dep[p] = d; for (auto q : edge[p]) if (!dep[p]) { dfs1 (q, d + 1 ); fa[q] = p; size += sz[q]; if (sz[q] > ma) hson[p] = q, ma = sz[q]; } sz[p] = size; }
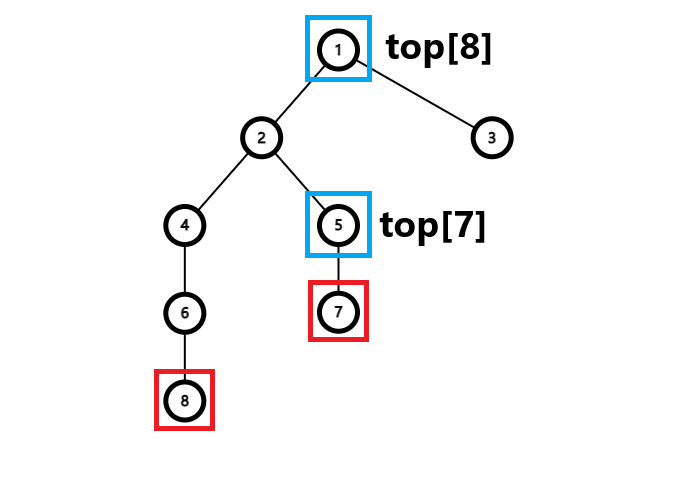
第二趟 每个节点的链头
注意,这里如果把根节点看做是轻节点,那么所有重链的链头都是轻节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 top[root] = root; void dfs2 (int p) for (auto q : edge[p]) { if (!top[q]) { if (q == hson[p]) top[q] = top[p]; else top[q] = q; } } }
求最近公共祖先 树链剖分可以单次
我们可以直接把链头深度较大的节点用其链头的父节点代替,然后继续求它与另一者的
由于在链上可以
1 2 3 4 5 6 7 8 9 10 11 12 int LCA (int a, int b) while (top[a] != top[b]) { if (dep[top[a]] > dep[top[b]]) a = fa[top[a]]; else b = fa[top[b]]; } return (dep[a] > dep[b] ? b : a); }
结合数据结构 在进行了树链剖分之后,我们便可以配合线段树等数据结构维护树上信息,这需要我们改一下第二次 每棵子树的最大 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 void dfs2 (int p) madfsn[p] = dfsn[p] = ++ cnt; if (hson[p]) { top[hson[p]] = top[p]; dfs2 (hson[p]); madfsn[p] = max (madfsn[p], madfsn[hson[p]]); } for (auto q : edge[p]) if (!top[q]) { top[q] = q; dfs2 (q); madfsn[p] = max (madfsn[p], madfsn[q]); } }
这段代码也太阴间了吧,别祸害其他人,第一个这么写的人也是牛的。——龙潜月十五、nottttttthy
所以给出两段正常而且简便的写法,上面那种写法是分情况讨论而且非常阴间的:
非分类讨论写法(大家经常是这么写的):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void dfs2 (int p, int fath) dfsn[p] = ++ dfsn[0 ]; top[p] = fath; rev[dfsn[0 ]] = a[p]; if (!hson[p]) return ; dfs2 (hson[p], fath); for (int i = head[p]; ~i; i = edge[i].nxt) { int v = edge[i].to; if (v == fa[p] || v == hson[p]) continue ; dfs2 (v, v); } }
分类讨论写法(我经常是这么写的,不过也不乏有人用这种方法):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void dfs2 (int p, int fath) if (hson[p]) { dfsn[hson[p]] = ++ dfsn[0 ]; top[hson[p]] = top[p]; rank[dfsn[0 ]] = hson[p]; dfs2 (hson[p], p); } for (int i = head[p]; ~i; i = edge[i].nxt) { int v = edge[i].to; if (!top[v]) { dfsn[v] = ++ dfsn[0 ]; rank[dfsn[0 ]] = v; top[v] = v; dfs2 (v, p); } } }
注意到,每棵子树的 ;而且,如果我们优先遍历重子节点,那么同一条链上的节点的
所以就可以用线段树等数据结构维护区间信息,例如接下来讲的路径修改,可以转化为线段树的区间修改。
路径修改 只要搞清楚转移和区间修改时端点就差不多了,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 inline void update (int x, int y, int z) while (top[x] != top[y]) { if (dep[top[x]] < dep[top[y]]) swap (x, y); update (1 , 1 , n, dfsn[top[x]], dfsn[x], z); x = fa[top[x]]; } if (dep[x] > dep[y]) swap (x, y); update (1 , 1 , n, dfsn[x], dfsn[y], z); }
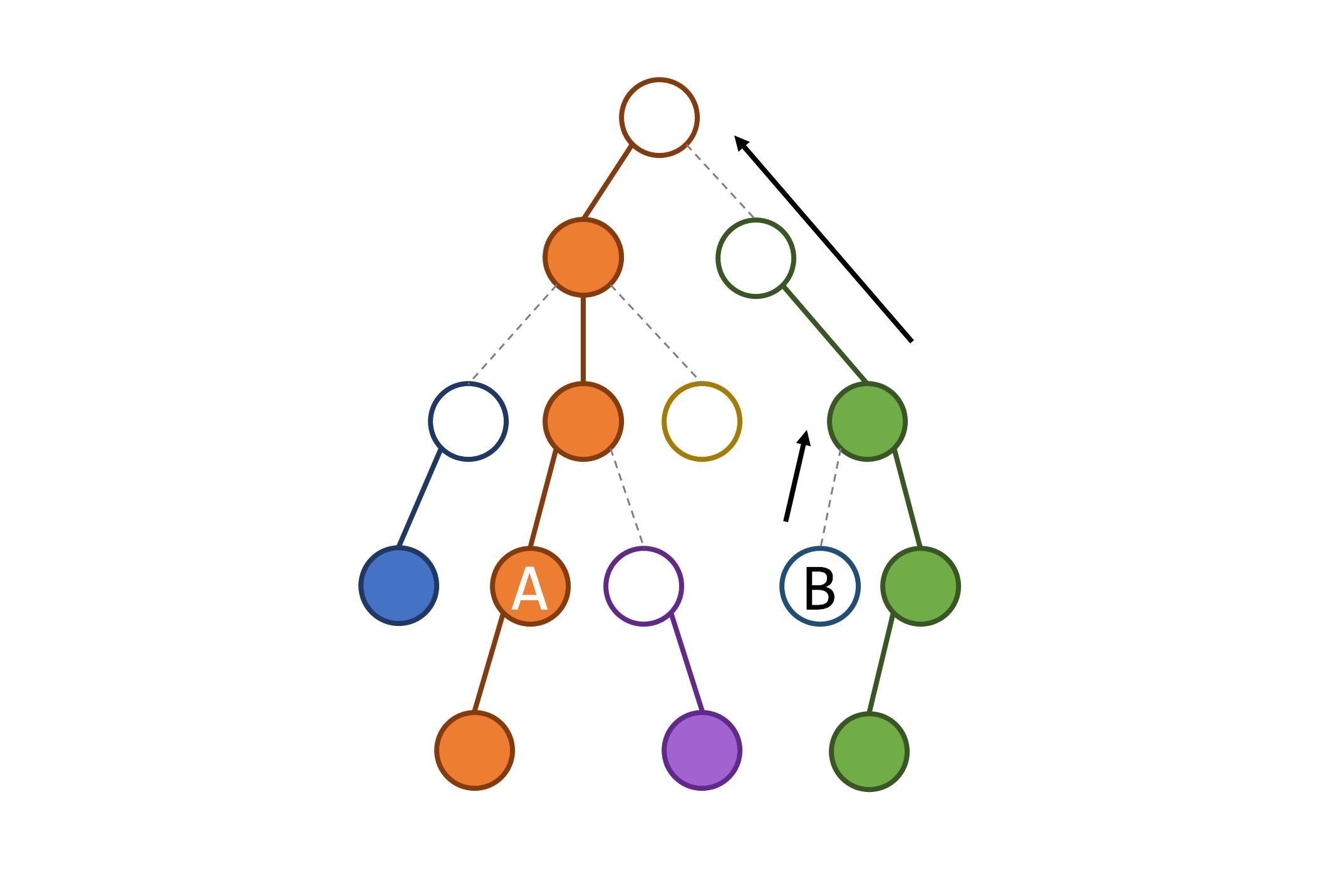
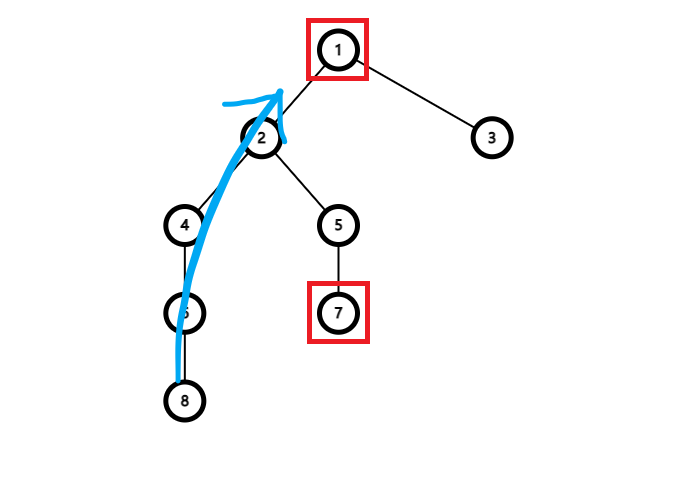
在未在同一条链时 ,为什么要让链头较深的点先往上跳?
假设我们现在要对着这张图幻想计算
那么我们看一下它们的链头在什么位置:
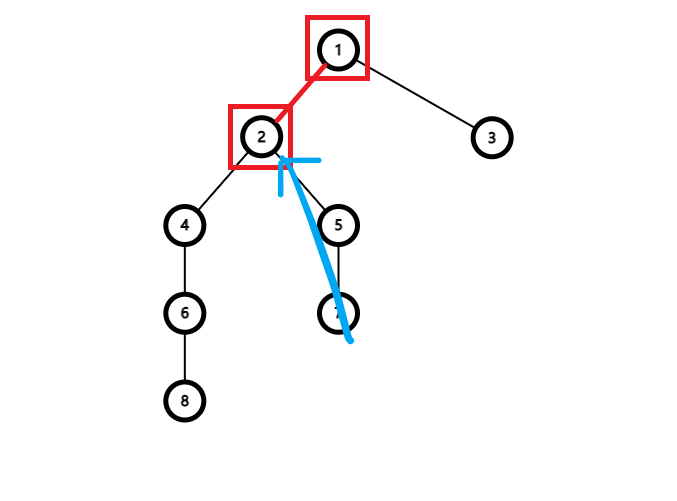
然后如果我们无所谓地跳,如果是让链头较浅的
那再让
我们发现,多出了一段
路径查询 与路径修改没啥区别,基本操作都交给线段树,我们树链剖分只负责给出区间。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 int query_path (int x, int y) int ans = 0 ; while (top[x] != top[y]) { if (dep[top[x]] > dep[top[y]]) { ans += query (dfsn[top[x]], dfsn[top[y]]); x = fa[top[x]]; } else { ans += query (dfsn[top[y]], dfsn[top[x]]); y = fa[top[y]]; } } if (dep[x] > dep[y]) ans += query (dfsn[y], dfsn[x]); else ans += query (dfsn[x], dfsn[y]); return ans; }
子树修改 如果是一棵子树,那么区间就是从这个点到叶节点,而叶节点恰是那个子树里
1 2 3 4 void update_subtree (int x, int z) update (dfsn[x], madfsn[x], z); }
子树查询 大概应该差不多几乎相同吧:
1 2 3 4 int query_subtree (int x) return query (dfsn[x], madfsn[x]); }
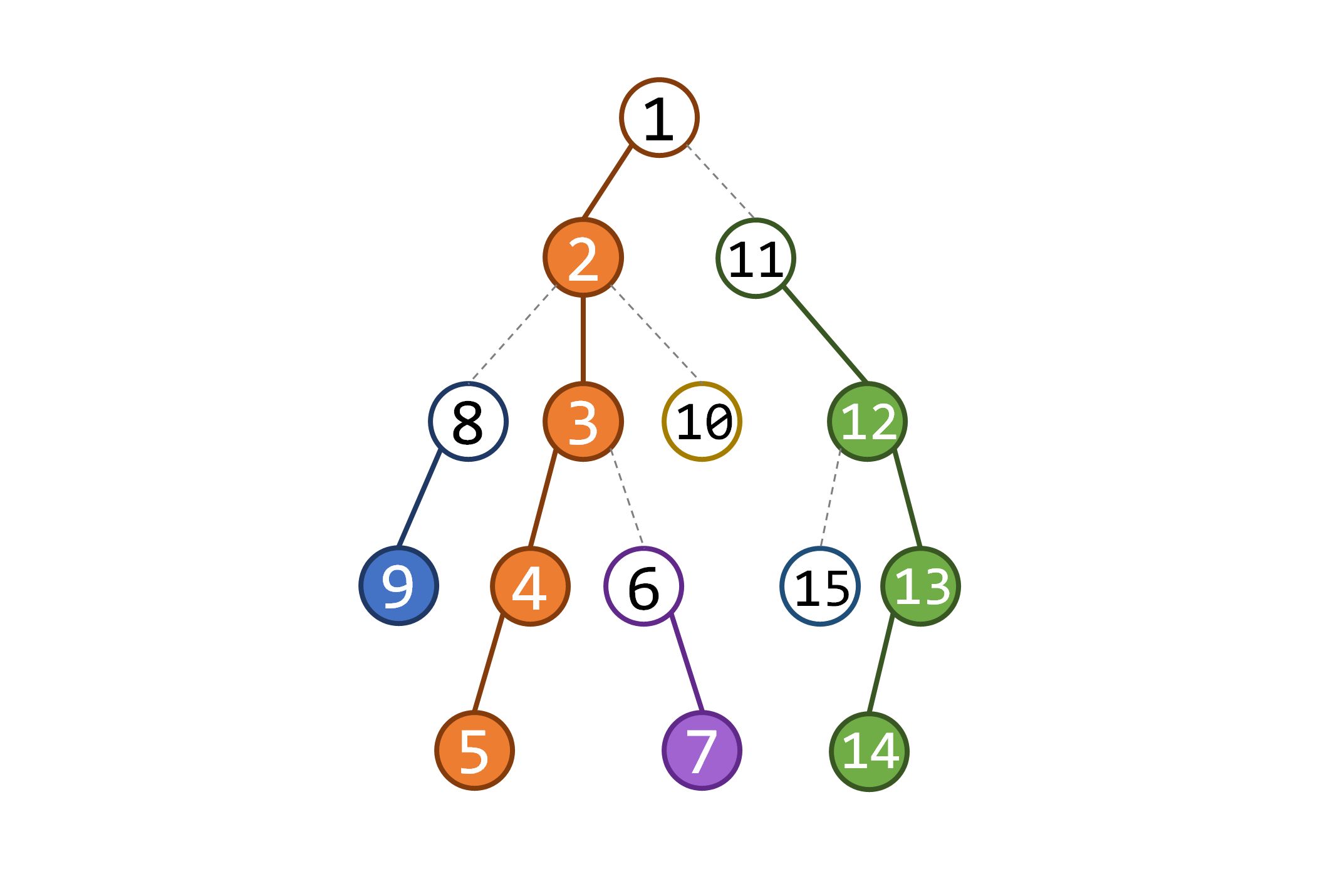
建线段树 需要注意,建线段树时要按
1 2 3 4 for (int i = 1 ; i <= n; i ++) scanf ("%d" , &b[i]); for (int i = 1 ; i <= n; i ++) a[dfsn[i]] = b[i];
当然,不仅可以用线段树维护,也可以用珂朵莉树等数据结构(很看数据),如果需要维护的是边权而不是点权,就把每条边的边权下放到深度较深的那个点就可,但是查询和修改的时候要记得略过最后一个点。
长链剖分
其实长链剖分和重链剖分没啥区别,但是看看名字都不一样所以定义也同样不同。
定义 重子节点 :表示其子节点中子树深度最大的子节点 ,如果有多个子树最大的子节点,取其一,如果没有节点就无重子节点。
轻子节点 :表示剩余的子节点。
重边 :这个节点到重子节点的边为重边。
轻边 :到其他轻子节点的边为轻边。
重链 :若干条首尾衔接的重边构成重链
然后你会发现其实我是直接把上面的那张图搬下来的,反正也符合长链剖分的法则。
所有链的长度的和都是 ,因为所有点在且仅在一条重链之中,永远只会被计算一次;任意一个点的 ,假如这个祖先的所在的重链长度小于
长链剖分的食用 代码其实也没啥不同,无非是我们的规则现在变成了子树深度最大的那个点作为重儿子。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 void dfs1 (int u, int fath) maxdep[u] = dep[u] = dep[fath] ++; fa[u] = fath; for (int head[u]; i; i = edge[i].nxt) { int v = edge[i].to; if (v == fath) continue ; dfs1 (v, u); if (maxdep[v] > maxdep[hson[u]]) { hson[u] = v; maxdep[u] = maxdep[v]; } } } void dfs2 (int u, int p) top[u] = p; len[u] = maxdep[u] - dep[top[u]] + 1 ; if (hson[u]) dfs2 (hson[u], p); for (int i = head[u]; i; i = edge[i].nxt) if (edge[i].to != fa[u] && edge[i].to != hson[u]) dfs2 (edge[i].to, edge[i].to); }
计算k次祖先 有好几种方法,可以树链剖分之后跳重链,这样是
然后其实最优可以达到预处理
代码老简单了,但是我就是不会:
1 2 3 4 5 6 7 8 9 10 inline int query (int x, int k) if (!k) return x; x = fa[x][log2[k]]; k -= 1 << log2[k]; k -= dep[x] - dep[top[x]]; x = top[x]; return k >= 0 ? nodeup[x][k] : nodedown[x][-k]; }