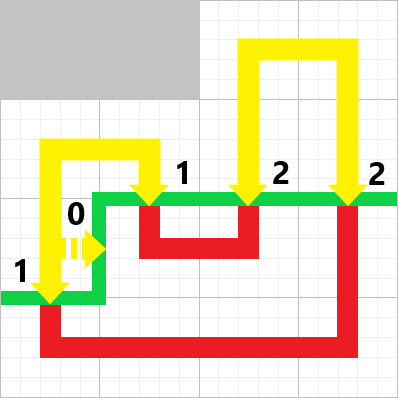
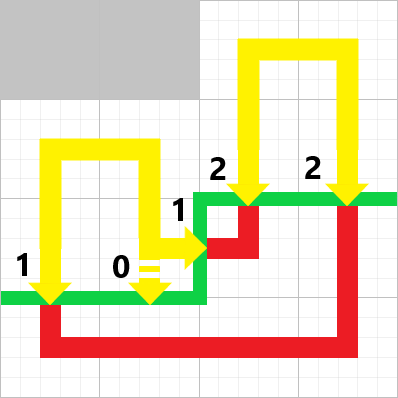
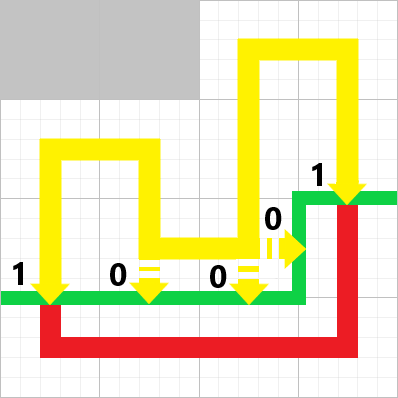
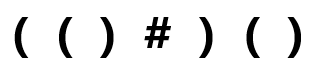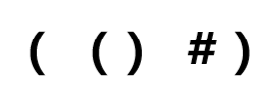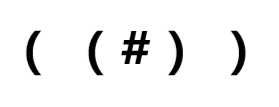就让我用这只手，将你那无聊的幻想杀得片甲不留。——《魔法禁书目录》

动态规划

动态规划（Dynamic Programming，DP），是运筹学的一个分支，是求解决策过程中最优化的过程。动态规划的应用及其广泛，包括工程技术、经济、工业生产、军事以及自动化控制等领域，并在背包问题、生产经营问题，资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果。

背包问题

背包问题（）是一种组合优化的 完全问题。其问题可以被简化成，给定一组物品，每个物品有自己的重量和价值，在限定的总重量里，如何选择使物品的总价值最大，也可以将背包问题描述成决定性问题，即在总重量不超过的前提下，总价值是否能到达？

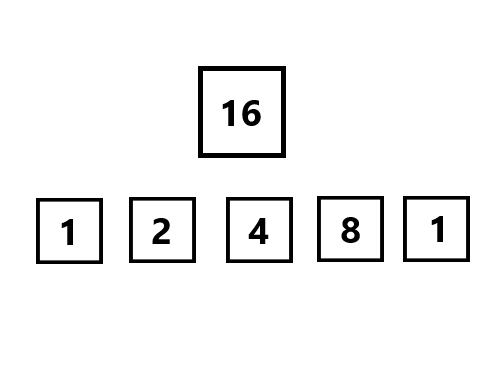
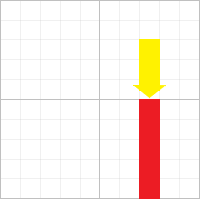
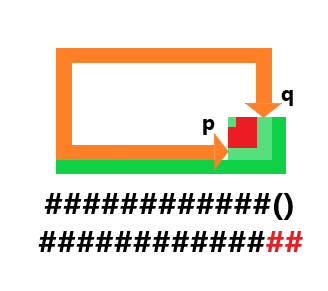
01背包

~~这是最简单的动态规划问题。~~

所谓 “ “ ，就是指每种物品只能选一次。

那么很显然，对于每个物品，只有拿或者不拿两者可能，对所有物品遍历，对于每个重量状态遍历，如果可以拿，就和不拿的情况进行对比，不拿就是不拿，仍等于前面的情况，所以就是~~拿就拿，不拿拉倒~~的一个简单思想。

那么尝试用表示在前件物品中，放入容量为的背包的最优解，那么就可以写出状态转移方程：

$f[i][j] = \max\lbrace f[i-1][j],f[i-1][j-weight[i]]+val[i]\rbrace$

模板代码如下：

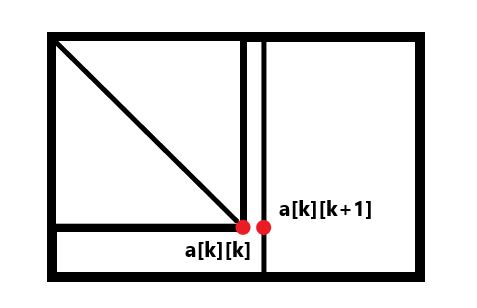
for (int i = 1; i <= n; i ++) // 遍历 n 件物品 
{
	for (int j = m; j >= 0; j --) // 遍历背包空间 m 
	{
		if (j >= w[i]) // 对于拿的情况，前提是剩余空间仍放的下  
			f[i][j] = max (f[i - 1][j], f[i - 1][j - w[i]] + val[i]); // 如果拿，就减去相应空间加上得到价值  
		else // 对于不拿的情况 
			f[i][j] = f[i - 1][j]; // 直接和前面相等就是了  
	}
}

对于拿，从拿和不拿的状态中选择一个更优的，如果拿，就从前面的状态减去相应的空间然后得到相应价值（也就是一份价钱一份货）。

~~对于不拿，不拿就是不拿，想拿都没法拿，怎么办也没法拿。~~

时间复杂度是，空间复杂度是，说起来其实都很糟糕所以我们要谈到滚动数组优化（可以滚来滚去骨碌骨碌转的数组哟~）

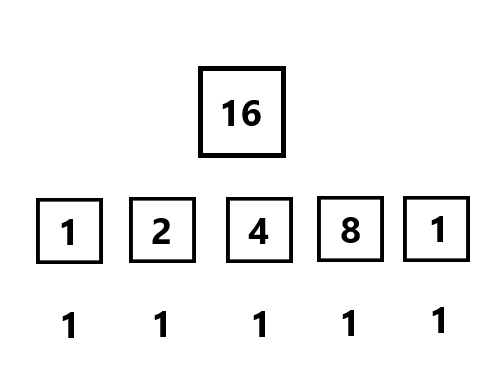
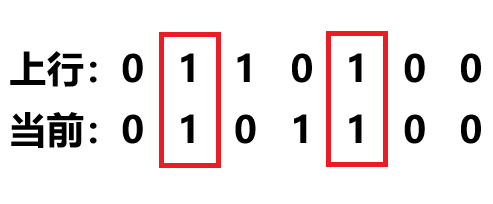
滚动数组

接下来我们要用一维数组代替掉非常糟糕的二维数组！

看到前面的状态转移方程：

1	f[i][j] = max (f[i - 1][j], f[i - 1][j - w[i]] + val[i]);

那么一个很显然的事实就是，为了得到现在的状态，需要知道和，由于我们使用二维数组保存中间状态，所以可以直接取出这两个状态。

当我们使用一维数组存储状态时，表示，在执行次循环后（已处理掉个物品），前个物品放到容量的最大价值。需要注意的是，第次循环的结果可能会覆盖掉次循环的结果。

为了求，我们需要知道前件物品放到容量为的背包中的最大贡献，即之前和前件物品放到容量为的背包中的贡献，即。

至于这里逆序枚举容量的原因，我们是由的状态推到的，而且，所以背包容量只有当 ~ 循环的时候才会先处理背包容量为の情况。

模板代码如下，似乎与前面别无二致：

for (int i = 1; i <= n; i ++) // 遍历 n 件物品
{
	for (int j = m; j >= 0; j --) // 遍历 m 空间
	{
		if (j > w[i]) // 如果放得下
			f[j] = max (f[j], f[j - w[i]] + v[i]); // 取最优解
		else 
			f[j] = f[j];
	}
}

我们之路的第一题应当是它：

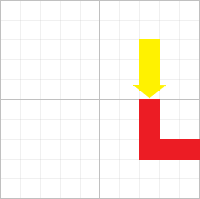
采药

山洞里有不同的草药，采摘每一株都需要不同的时间，每一株都有其自身的价值，每种草药只能采摘一次，问能在给定时间内能采到草药最大的价值。

因为是背包的板子题，直接上代码了，或者你也可以尝试着直接把模板代码交上去，兴许能对呢。

for (int i = 1; i <= n; i ++) // 遍历 n 件物品 
{
	for (int j = m; j >= w[i]; j --) // 遍历背包空间 m 
	{
		f[j] = max (f[j], f[j - w[i]] + v[i]); // 选择更优情况   
	}
}

常数优化

当我们在枚举空间时，有如下优化：

1	for (int j = m; j >= max (m - (sumw[n] - sumw[i]), v[i]));

其中表示，即物品重量前缀和。这一重循环的伪代码即：

$j \leftarrow m\ to \max(V-\sum_{i}^{N}w[i], w[i])$

大概意思是当很大时，可以将从第个到后面的所有物品全部装入背包且剩余空间还大于第个物品空间时，可以减少不必要的循环，还有一些文章认为可以把这个循环严格优化到。

bitset 优化

这个优化通常是用于那些需要涉及集合的题目的，但是不学又不行，我也不想学呀，有什么办法呢。

这里废话我们不讲，教学左转好吧。

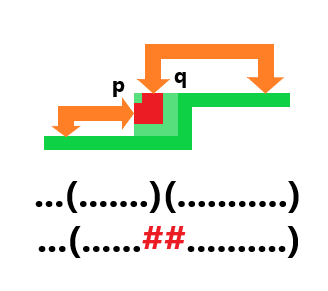
完全背包

~~这是最简单的动态规划问题。~~

似乎这个问题非常の不切实际的，问题建立在什么物品都能无限拿（所谓“完全”）的环境中，在不超过空间的前提下，问最大的贡献。

那么策略就不是单纯地拿或者不拿了，进化到了拿件，拿件……拿的多种决策。那么我们仍可以使用解背包的思想，令表示在前件物品中选择放入容量为的背包的最优解，那么就可以写出状态转移方程：

$f[i][j]=\max\lbrace f[i-1][j],f[i-1][j-k\times w[i]]+k\times val[i]\rbrace\ \ \ (1 \leq k \leq \lfloor\frac{m}{w[i]}\rfloor)$

如果此时取，也就是不取这件物品，那么方程就可以写成：

$f[i][j]=f[i-1][j-k\times w[i]]+k\times val[i]\ \ \ (0 \leq k \leq \lfloor\frac{m}{w[i]}\rfloor)$

模板代码如下：

for (int i = 1; i <= n; i ++) // 遍历物品 
{
	for (int j = m; j >= 0; j --) // 遍历空间 
	{
		for (int k = 0; k * w[i] <= j; k ++) // 遍历拿 k 次 
		{
			f[i][j] = max (f[i][j], f[i - 1][j - k * c[i]] + k * val[i]);
		}	
	}
}

当然也可以写成这样（同时优化了空间）：

for (int i = 1; i <= n; i ++) // 遍历物品 
{
	for (int j = m; j >= 0; j --) // 遍历空间 
	{
		for (int k = 0; k * w[i] <= j; k ++) // 遍历拿 k 次 
		{
			f[j] = max (f[j], f[j - k * c[i]] + k * val[i]);
		}	
	}
}

在这段代码里，如果这个物品的重量已经超过了剩余重量，即的情况下，就不会被选择了，这也是为什么正序循环的原因。

求解一个状态的时间复杂度是总的时间复杂度是。

这里给出一个《采药》的进阶版例题：

疯狂的采药

山洞里有不同的草药，采摘每一株都需要不同的时间，每一株都有其自身的价值，每种草药能采摘无限次，问能在给定时间内能采到草药最大的价值。

可以直接交一发模板代码（要开），肯定能对，不对我也没辙：

for (int i = 1; i <= n; i ++) 
{
	for (int j = w[i]; j <= m; j ++) 
	{
		f[j] = max (f[j], f[j - w[i]] + val[i]);  
	}
}

优化

这里可以想到一个简单有效的优化，若两件物品和满足且，则就可以将物品直接去掉，不用考虑，正确性是显然的，我总不可能拿一件又重还没有价值的物品，都说了一份价钱一分货对吧。

转化

~~世界线收束。~~，我们可以把完全背包转为背包求解。

显然，在完全背包中，第种物品最多能拿件，于是可以将其转化成件价值均不变的物品，然后对其求解，不过完全没有减少时间复杂度。

更高效的还可以采用二进制思想，把第种物品拆成费用为、价值为的若干件物品，其中取遍满足的非负整数，可以把每种物品拆成件物品。

时间优化

上联：前面的复杂度很大，我们还是要来优化。

下联：如果你觉得这个算法很差，请你来掉它。

横批：代码如下。

for (int i = 1; i <= n; i ++) // 遍历 n 件物品 
{
	for (int j = w[i]; j <= m; j ++) // 遍历空间  
	{
		f[j] = max (f[j], f[j - w[i]] + val[i]); // 详情请垂询下面的解释  
	}
}

观察，这份代码和背包的代码只有第二层循环的差别（一个是正序，一个是倒序）。

背包循环倒序是因为保证第循环的最优解能由第次推过来，需要绝无已经选入第件物品的子结果即，保证每件物品只选一次。而现在每种物品能选无限件，考虑“选入第件物品”的策略时，是“加选第种物品”，需要从可能已选入子结果 来推，所以要利用正序。

时间复杂度是。

多重背包

~~这是最简单的动态规划问题。~~

这是一个比背包和完全背包更加真实的背包问题，多重背包限定了每种物品的个数。

现在对于每个物品有种策略：取件，取件……取件，令表示前种物品放入容量为的背包的最优解。

根据前面的经验，我们只要偷个懒把前面的方程改一下就可以了，现在方程是这样的：

$f[i][j]=f[i-1][j-k\times w[i]]+k\times val[i]\ \ \ (0 \leq k \leq s[i])$

复杂度是。

转化

~~世界线再次收束。~~

和前面转化的思想一样，把第种物品转化成件价值均为，代价均为的物品，是不是和前面很像？

时间复杂度仍没有改变，还是。所以我们采用二进制思想，把每种物品的个数拆成这类形式，价值均相等，然后跑一遍背包就可以了，二进制化代码如下：

for (int i = 1; i <= n; i ++) // 对 n 个物品遍历  
{
	int x = 1; // 从 1 开始 
	while (s[i] >= x) // 在数量还有的情况下继续二进制化  
	{
		s[i] -= x; // 和普通二进制化差不多吧  
		g[++ cnt].w = x * w[i]; // 弄到一个新的数组里去  
		g[cnt].v = val[i] * x; // 这里垂询下面的解释 
		x <<= 1; // 往上抬  
	}
	if (s[i] > 0) // 二进制化后剩下的数字  
	{
		g[++ cnt].w = s[i] * w[i]; // 同上 
		g[cnt].v = val[i] * s[i]; // 同上 
	}
}

第一个问题，对于这段代码：

1	g[cnt].v = val[i] * x; // 这里垂询现在的解释

对于一个被“解剖”的物品部分将其看做一坨东西，假设现在有个一样的价值为的东西：

来模拟！

那么我们将其二进制化以后，还留下来一个，保证从 ~ 的每一种个数都能被拿到，所以刚刚的说辞可以转化为这张图，我将每个块都看做一个物品，最终从个物品转化得到了个物品，那么相应的它们的价值就是，最后也可以说成是有个物品，然后每个物品都有一种，价值就是：

将每个块块看做一个块

比如说上面那张图，第二个块就是一个价值为的物品。

分组背包

~~这是最简单的动态规划问题。~~

这是一个还算比较真实的问题，但是没有多重背包真实，而且你甚至能把它代到游戏等环境中？

对于所有背包，将其分成组，对于第组物品，只能选择其中的一种物品（组内物品冲突），且对于这种物品只能是选或不选两种策略。

比较朴素的想法是，遍历共组，对于每组的每件物品选择取或不取，取遍历下一组，不取就遍历这一组的下一件物品，令表示前组物品放入容量为的背包的最优解，则有以下公式：

$f[i][j]=\max\lbrace f[i-1][j],f[i-1][j-w[i]]+val[i]\mid item\ i \in group\ k\rbrace$

代码如下：

for (int i = 1; i <= k; i ++) // 遍历 k 组 
{
	for (int j = m; j >= 0; j --) // 遍历空间  
	{
		for (int l = 1; l <= s[i]; l ++) // 遍历第 i 组的 
		{
			int x = a[i][l]; // 记一下第 i 组第 l 个的物品编号 
			if (j >= w[x]) // 如果放的下  
			{
				f[j] = max (f[j], f[j - w[x]] + val[x]); // 取最优解  
			}
		}
	}
}

三层循环的顺序保证了每一组内的物品最多只有一个被加入到背包中。

二维费用背包

~~这是最简单的动态规划问题。~~

前面我们可能活在一个牛顿不在的世界，物品竟然是没有体积只有质量的，难以置信。

现在的物品多了一个属性，即容积，二维费用背包问题就是给定背包的最大容积和最大载重，给定每种物品的容积，质量和数量，数量的话其实是不重要的，因为我们可以靠拆来将其转化为背包，但其本质还是二维费用背包。

既然换了个世界，就要多加一维，那么状态也多加一维，状态转移方程如下：

$f[i][j][k]=\max\lbrace f[i-1][j][k],f[i-1][j-v[i]][k-w[i]]+val[i]\rbrace$

当每件物品只能取一次时，让体积和容量采用逆序的循环，完全背包时采用顺序的循环，多重背包时拆分物品。

for (int i = 1; i <= n; i ++) // 遍历 n 个物品  
{
	for (int j = W; j >= 0; j --) // 倒序，完全背包时正序 
	{
		for (int k = V; k >= 0; k --) // 倒序，完全背包时正序  
		{
			f[j][k] = max (f[j][k], f[j - w[i]][k - v[i]] + val[i]);
		}
	}
}

依赖背包

~~这是最简单的动态规划问题。~~

~~这种背包问题的存在是因为某些病毒软件，下了这个又要给你下它本家的所有东西，它本家的东西又要给你下别的病毒软件的东西。~~

：你干脆报我户口算了。

问题中的物品间存在某些“依赖”关系。也就是说物品依赖物品，表示若选物品，就必须选择。按照背包问题一般的思路，考虑每个主件和其附件的集合，但是可用的策略很多，可以一个都不选，仅选择主件，选择其主件的一个附件，选择两个附件……用状态转移方程无法表示那么多的策略。事实上，设有个附件，则策略有个，为指数级。

考虑到所有策略都是互斥的（也就是只能选择一种策略），所以一个主件和它的附件可以被看做一个分组背包中的一组。代码如下：

for (int i = 1; i <= k; i ++) // 遍历 k 组选择
{
	for (int j = m; j >= 0; j --) // 遍历空间  
	{
		for (int l = 1; l <= s[i]; l ++) // 遍历第 i 组主件与附件 
		{
			int x = a[i][l]; // 记一下第 i 组第 l 个的物品编号 
			if (j >= w[x]) // 如果放的下  
			{
				f[j] = max (f[j], f[j - w[x]] + val[x]); // 取最优解  
			}
		}
	}
}

当然对于一些选择策略比较少的题目（如《金明的预算方案》，也可以考虑使用背包完成）。

有一部分依赖背包的多种决策是在取完前一种才能取的，同样也给了我们另一个思路来存组内决策，如这题：

黄金矿工

边缘正在玩黄金矿工，现在他想要在时间内从个黄金中获得最大价值，他可以在瞬间将钩子转向一个角度，给出个黄金的坐标，价值和挖到需要的时间，有些黄金的坐标在同一条线上，此时需先拿最前面的黄金。

这里可以用到笛卡尔坐标系来算斜率判哪些黄金在同一条线上，同时使用排序降低难度，将其放进一组，然后因为对于一条线上的黄金（一组里的）拿后面那个黄金的前提是拿前面的黄金（体现其依赖性），所以它的价值就是加上它的价值，花费亦是如此，然后简单跑一个分组背包应该不是问题，完整代码如下：

#include <bits/stdc++.h>

using namespace std;

const int N = 2e3 + 1;
int n, t, cnt;
int s[N], v[N][N], ti[N][N], f[40001];

struct Gold { \\ 黄金结构体
	int x, y, t, val;
	double k; // 斜率
} a[N];

inline bool cmp (Gold p, Gold q)
{
	return p.k == q.k ? p.y < q.y : p.k < q.k;
}

int main ()
{
	scanf ("%d %d", &n, &t);
	for (int i = 1; i <= n; i ++)
	{
		scanf ("%d %d %d %d", &a[i].x, &a[i].y, &a[i].t, &a[i].val);
		a[i].k = a[i].y * 1.0 / (a[i].x * 1.0); // 算斜率，方便排序
	}
	sort (a + 1, a + n + 1, cmp); // 条件快排
	for (int i = 1; i <= n; i ++)
	{
		if (a[i].k != a[i - 1].k || i == 1) // 如果不等于前面那个或者还只是第一个
			++ cnt; // 重开个组
		if (!s[cnt]) // 如果这一组的数量为 0 ，第一个不需要叠加价值
		{
			v[cnt][++ s[cnt]] = a[i].val;
			ti[cnt][s[cnt]] = a[i].t;
		}
		else // 对于这条线（一组）上后面的黄金
		{
			++ s[cnt];
			v[cnt][s[cnt]] = v[cnt][s[cnt] - 1] + a[i].val;
			ti[cnt][s[cnt]] = ti[cnt][s[cnt] - 1] + a[i].t;
			// 关键，叠加价值和花费来作为一个组内的决策，而不是像《金明的预算方案》一样可以随便选  
		}
	}
	for (int i = 1; i <= cnt; i ++) // 遍历组数 
		for (int j = t; j >= 0; j --) // 遍历空间  
		{
			int maxn = f[j]; // 对于每一组的最佳选择，这里初始为不选  
			for (int k = 1; k <= s[i]; k ++)
				if (j >= ti[i][k])
					maxn = max (maxn, f[j - ti[i][k]] + v[i][k]);
			f[j] = maxn;
		}
	printf ("%d", f[t]);
}

泛化物品

~~这是……啊，不对，这好像不是动态规划问题啊……~~

考虑这样一种物品，它并没有固定的费用和价值，而是它的价值随着你分配给它的费用而变化。

更严格的定义。在背包容量为的背包问题中，泛化物品是一个定义域为中的整数的函数，当分配给它的费用为时，能得到的价值就是。另一种是理解是把这种物品比作一个数组，给定一个，得到的价值就是。

一个费用为价值为的物品，如果它是背包中的物品中的物品，那么把它看做泛化物品，它就是除了其他函数值都是的一个函数；如果它是完全背包中的物品，那么它就是一个仅当被整除时有其他函数值均为的函数；如果它是多重背包中重复次数最多为的物品，那么它对应的泛化物品的函数有仅当被整除且，其他情况均为；分组背包中的物品组，也可看做泛化物品。

如果给定了两个泛化物品和，要用一定的费用从这两个泛化物品中得到最大的价值，只需枚举费用给这两个物品即可，有点像二次函数：

$f(v)=\max\lbrace h(k)+l(v-k)\mid 0 \leq k \leq v\rbrace$

因为这里的是由泛化物品和决定的定义域为的函数，所以也可以说，是一个由泛化物品和决定的泛化物品。

到达背包

~~这是最简单的动态规划问题。~~

对于一种是否能完成一个任务的题目，令表示第物品，当前空间为时能否完成这个任务，在最后的时候再遍历得到最大解。

这里给出例题：

音量调节

一个吉他手决定参加一场表演，每表演一首歌前他必须改变一次音量，可以是降低或升高，最低不可以低于分贝，最高不可以高于分贝，他想用最大音量演奏最后一首歌，现给出演奏每首歌前可以改变的音量，最高分贝，刚开始的音量和歌的数量，如果他可以做到就输出最大分贝，如果不彳亍就输出“ ”。

这题不可以使用滚动数组，其他就等于是模板吧，只是状态里存的是现在是否可行就是了：

#include <bits/stdc++.h>

using namespace std;

int n, maxn, x; 
int a[51], f[51][1001];

int main ()
{
	scanf ("%d %d %d", &n, &x, &maxn);
	f[0][x] = 1; // 最开始的时候必定可行  
	for (int i = 1; i <= n; i ++)
		scanf ("%d", &a[i]);
	for (int i = 1; i <= n; i ++) // 遍历物品  
	{
		for (int j = maxn; j >= 0; j --) // 以音量大小作为背包空间 
		{
			if (j - a[i] >= 0) // 如果不会低于 0
				f[i][j] = f[i][j] || f[i - 1][j - a[i]]; // 从两者中选择可行状态（其实是有一个可行就行） 
			if (j + a[i] >= 0) // 如果不会高于最大音量
				f[i][j] = f[i][j] || f[i - 1][j + a[i]]; // 同上 
		}
	}
	for (int i = maxn; i >= 1; i --)
		if (f[n][i]) // 对于一个可行的已经到达第 n 个物品输出其最大价值 
			return cout << i, 0;
	return cout << -1, 0; 
}

进程背包

~~这是最简单的动态规划问题。~~

对于这种加工调换过程的，这其中的有些题目也可以当做背包来做，比如这题：

产品加工

某加工厂有和两台机器，加工的产品可以在其中任何一个机器完成，或两台机器共同完成，不同机器加工不同产品的时间不同，现给定个产品加工的各个时间，合理安排任务的调度顺序，使时间最短。

特别的，当一个时间为时表示不能使用方案加工产品。

开始先设计状态，表示机器用时为时，机器的最短用时，这里把答案当做状态转移，然后可以推出以下方程：

$f[i][j]=\min\left\lbrace \begin{aligned}{} &{f[i-1][j-t_i.a]}\\\\ &{f[i-1][j]+t_i.b}\\\\ &{f[i-1][a-t_i.c]+t[i].c}\\\\ \end{aligned} \right.$

代码如下：

#include <bits/stdc++.h>

using namespace std;

int n, m, ans = 0x7fffffff, down, up, f[30001];

inline int max (int x, int y)
{
	return x > y ? x : y;
}
inline int min (int x, int y)
{
	return x < y ? x : y;
}

int main ()
{
	scanf ("%d", &n);
	for (register int i = 1; i <= n; i ++)
	{
		int a, b, c;
		scanf ("%d %d %d", &a, &b, &c);
		m = down;
		down = 0x7fffffff;
		up += max (a, max (b, c)); // 用最大时间来决定上界 
		for (register int j = up; j >= m; j --)
		{
			int tmp = 0x7fffffff;
			if (a && j - a >= m) // 如果可以拿
				tmp = min (tmp, f[j - a]);
			if (b)
				tmp = min (tmp, f[j] + b);
			if (c && j - c >= m)
				tmp = min (tmp, f[j - c] + c);
			if (tmp < 0x7fffffff)
				down = min (down, j); // 更新下界
			f[j] = tmp; // 最优解
		}
	}
	for (int i = down; i <= up; i ++)
		ans = min (ans, max (i, f[i]));
	printf ("%d\n", ans);
	return 0;
}

分数规划背包

~~这是最简单的动态规划问题。~~

写到下面例题的时候突然遇到了，所以跑上来补一下。

分数规划问题

首先随便讲讲分数规划问题。

对于一个集合，必须遵守某种组合关系，求在这些元素中选出一些记作新集合并且使得最大或最小。

然后这种问题使用的通常是二分法或者算法，闲得蛋疼的时候我估计会去学这俩东西。

啊还有什么各种模型比如最优比率树啦，最优比率环啦，最大密度子图啦，这种东西都不重要的晓得哇，天塌下来我都不会去学。

例题

阿米娅的儿童节礼物

可露希尔的商店里有件商品，每个商品有两个属性，价钱和实用度，现在博士你要买若干个物品当做送给阿米娅的礼物，礼物的心意值为买的物品实用度的和，然后礼物的价值就是买的物品价钱的和。

博士希望礼物的心意值恰好是价值的倍，请计算身为巴别塔的恶灵的你送出礼物的最大心意值。

先拆柿子：

$\frac{\sum_{i=1}^na_i}{\sum_{i=1}^nb_i}=k$ $\sum_{i=1}^n(a_i-b_i\times k)=0$

所以我们就可以使用分数规划的老套路：

$c_i=a_i-b_i\times k$

再以为质量，为价值进行背包即可。

需要注意的是，由于可能为负数，我们要设两个数组，令表示质量和为时的最大价值，令表示质量和为时的最大价值，然后用统计答案。

给出代码~当当了当：

#include <bits/stdc++.h>

using namespace std;

const int N = 2e4 + 1;

int n, k, f[N], g[N];

int a[N], b[N], c[N], ans;

int main ()
{
	scanf ("%d %d", &n, &k);
	for (int i = 1; i <= 1e4 + 1; i ++)	
		f[i] = g[i] = -1e9;
	for (int i = 1; i <= n; i ++)
		scanf ("%d", &a[i]);
	for (int i = 1; i <= n; i ++)
		scanf ("%d", &b[i]);
	for (int i = 1; i <= n; i ++)
	{
		c[i] = a[i] - b[i] * k;
		if (c[i] >= 0)
			for (int j = 1e4; j >= c[i]; j --)
				f[j] = max (f[j], f[j - c[i]] + a[i]);
		else
			for (int j = 1e4; j >= -c[i]; j --)
				g[j] = max (g[j], g[j + c[i]] + a[i]);
	}
	for (int i = 0; i <= 1e4; i ++)
		ans = max (ans, f[i] + g[i]);
	if (ans > 0)
		printf ("%d\n", ans);
	else
		puts ("-1");
	return 0;
}

时间排序背包

~~这是最简单的动态规划问题。~~

自己起的名字，其实只是一个背包的变种而已，废话不多说我们直接来看例题：

抢救物资

有人的房子着火了，他想从大火中带走价值总和尽量多的物品，每次他只能带走一个，分别给出挽救某物品需要的时间，该物品开始燃烧的时间（从该时间开始就不能挽救该物品了），物品的价值。

非常的，你可以看出这是一个背包问题对吧，而且似乎只是把时间用做了背包空间。

但是在此之前先让我们给物品按照开始燃烧的时间排序，这样才能满足无后效性。

然后就按照正常背包做吧，代码给出：

for (int i = 1; i <= n; i ++)
	for (int j = a[i].d - 1; j >= a[i].t; j --)
		if (f[j - a[i].t] + a[i].val > f[j])
		{
			f[j] = f[j - a[i].t] + a[i].val;
			res[j] = res[j - a[i].t];
			res[j].push_back (a[i].id);
		}

区间动态规划

~~这是最简单的动态规划问题。~~

区间是线性动态规划的拓展，它在分阶段地划分问题时，与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系，那么既然是在区间上，我们可以随便设一个最基础的状态表示区间到的最优解。

对于一个区间中，比较常规的想法是将其分成和两部分进行求解，可以写出如下最基础的状态转移方程：

$f[i][j]=\max\lbrace f[i][k]+f[k+1][j]+cost\rbrace$

其中是将两区间合并起来的代价。

先从一道简单的题目入手：

石子合并

在一个环上摆放坨石子，现要将石子有次序的合并成一坨，规定每次只能选相邻两坨合并，并将新的一坨石子数，记为本次合并的分数，求合并结束后的最小分数和最大分数。

看到环，首先断环成链得到一个两倍的数组，再令表示从第堆到第堆的最优解，用一个指针在区间中移动分割区间，可以得到以下状态转移方程：

$f[i][j]=\max\lbrace f[i][k]+f[k+1][j]+\sum_{t=i}^ja_t\rbrace\ (i \leq k \leq j)$

这里可以采用前缀和预处理出区间的石子个数，令表示区间的石子数，就可以把方程写成这样：

$f[i][j]=\max\lbrace f[i][k] + f[k+1][j]+sum_j-sum_{i-1}$

for (int i = 1; i <= n; i ++) // 枚举长度  
{
	for (int j = 1; i + j <= 2 * n; j ++) // 区间左端点  
	{
		int end = i + j - 1; // 区间右端点  
		for (int k = j; k < end; k ++) // 从 j 到 end 枚举 k 指针 
		{
			f1[j][end] = min (f1[j][end], f1[j][k] + f1[k + 1][end] + sum[end] - sum[j - 1]);
			f2[j][end] = max (f2[j][end], f2[j][k] + f2[k + 1][end] + sum[end] - sum[j - 1]);
		}
	}
}

此时的时间复杂度是。

当然对于一些回文字符串的题目，区间也是一种不错的方法。

天王老子来我都不学马拉车

给定一个由小写字母组成的字符串，给出询问，每组询问给定一个二元组，问字符串区间的子串中，包含多少回文串。

时间给的老长了，而且空间也不小，所以我们可以往死里开。

然后可以确定状态是表示中的回文串数量，那么就可以使用讲得很好听的中心扩散法，也就是弄两个指针往外判是不是回文串。

然后为了方便理解我们来把样例” “得到的每个状态值做成一个表格看着玩玩：

嗯……总感觉……

然后你可能会觉得似乎是有点规律的但其实好像是没有规律的（我在说什么我靠）。

回文子串是有奇数和偶数长度两种情况，所以两种都要算。

给出代码：

#include <bits/stdc++.h>

using namespace std;

const int N = 5e3 + 1;

char s[N];

int f[N][N], n, q;

int main ()
{
	scanf ("%s", s + 1);
	scanf ("%d", &q);
	n = strlen (s + 1);
	for (int i = 1; i <= n; i ++)
	{
		for (int j = i, k = i; j && k <= n && s[j] == s[k]; j --, k ++)
			f[j][k] ++;
		for (int j = i, k = i + 1; j && k <= n && s[j] == s[k]; j --, k ++)
			f[j][k] ++;
	}
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= n; j ++)
			f[i][j] += f[i][j - 1] + f[i - 1][j] - f[i - 1][j - 1];
	for (int l, r; q --;)
	{
		scanf ("%d %d", &l, &r);
		printf ("%d\n", f[r][r] - f[l - 1][r] - f[r][l - 1] + f[l - 1][l - 1]);
	}
	return 0;
}

诶你可能会说上面这个题目不够回文串，那我再来一道回文串题目：

祖玛游戏

祖玛游戏里，存在个一行的宝石，第个宝石的颜色为，游戏的目标是尽快地消灭一行中所有的宝石。在一秒钟，能很快的挑选出有颜色的宝石中的一个回文的，连续的子串，并将这个子串移除。每当一个子串被删除后，剩余的宝石将连接在一起，形成一个新的行列，求出把整个宝石串都移除的最短时间。

（其实原祖玛只要三颗珠子连在一起了就会自己消掉）

呃……这个其实就是推式子，然后通常都是表示区间的最少次数。

然后可以想到，对于一个珠子，代价就是，由此。

对于相邻的珠子，如果它们俩相同，代价就是，即，如果不相同，代价就是，即。

那么初始化就是这样，然后我们去一步步弄出大区间，那么对于一个宝石串而言，如果两端相同，代价和加不加这两端是一样的，所以可以由前面那个推出来，即，至于这边为什么是和的话，是因为从到，高兴你也可以到。

然后记得套区间的板子！因为要由两端相接的区间合成一个大区间！代码如下：

#include <bits/stdc++.h>

using namespace std;

const int N = 501;
const int inf = 20050409; // 这个很大麽  

int n, a[N], f[N][N];

int main ()
{
	scanf ("%d", &n);
	for (int i = 1; i <= n; i ++)
		scanf ("%d", &a[i]);
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= n; j ++)
			f[i][j] = inf; // 因为后面有最小值操作所以开始直接赋成超级大 
	for (int i = 1; i <= n; i ++)
		f[i][i] = 1;
	for (int i = 1; i < n; i ++)
	{
		if (a[i] == a[i + 1])
			f[i][i + 1] = 1;
		else
			f[i][i + 1] = 2;
	}
	for (int i = 3; i <= n; i ++) // 枚举长度，从 3 开始（前面已经得到过 2 的情况了哦） 
	{
		for (int j = 1; i + j - 1 <= n; j ++) // 枚举出发点！ 
		{
			int l = j, r = i + j - 1; // 左端点和右端点  
			if (a[l] == a[r])
				f[l][r] = f[l + 1][r - 1];
			for (int k = l; k < r; k ++)
				f[l][r] = min (f[l][r], f[l][k] + f[k + 1][r]); // 合成大区间  
		}
	}
	printf ("%d", f[1][n]); // 最后答案就是一整段的答案了 
	return 0;
}

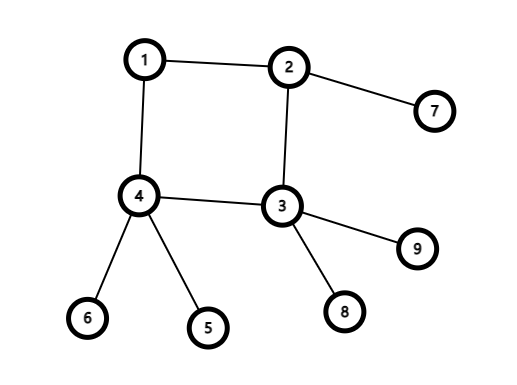
树形动态规划

由于树固有的递归性质，树形动态规划一般都是递归进行的。

一般来说树形在设状态转移方程时都可以用表示以为根的子树最优解，实现时一般用子树更新父亲（从下至上，很像革命）。对于一般的树形，我们需要把所有子树的信息都掌握完了再更新父亲；而树形背包就需要一个一个更新，每次都用一个子树更新已经更新过的子树和父亲，最后可以把这一部分的子树更新完，再向上更新，最后根节点存的就是答案。

基础

~~这是……额……反正有例题！那就是最简单的动态规划问题了！~~

我们从一道老生常谈的题开始，《没有上司的舞会》：

没有上司的舞会

某大学有个职员，编号为 ~ 。他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数，但是如果某个职员的上司来参加舞会，那么这个职员就不会参加宴会。问邀请哪些职员能得到最大的快乐指数。

可以定义表示以为根的子树的最优解（第二维的值表示上司不参加舞会，表示参加）

显然，我们可以推出两个状态转移方程：

$f[i][0]=\sum\max\lbrace f[x][0],f[x][1]\rbrace$

第一个方程，对于上司不来的情况，下属可以选择来或不来，那么在其中选择最优解，统计子树答案。

$f[i][1] = \sum f[x][0] + a[i]$

第二个方程，对于上司来的情况，下属都不会来，对这个状态加上上司的快乐指数，加上子树的答案。

通过，在返回上一层时更新当前节点的最优解，代码如下：

void dfs (int p) // 传入当前节点
{
	vis[p] = 1; // 记录被访问
	for (int i = head[p]; i; i = edge[i].nxt) // 前向星遍历
	{
		if (vis[edge[i].to]) // 如果终点已查过
			continue; // 直接退出
		dfs (edge[i].to); // 向下递归
		f[p][1] += f[edge[i].to][0]; // 统计
		f[p][0] += max (f[edge[i].to][0], f[edge[i].to][1]); // 取最优解
	}
	return ;
}

还有一道处理方法更普遍的题目，《二叉苹果树》

二叉苹果树

有一棵苹果树，树枝必分为两叉，这棵树共有个节点（叶子点或者树枝分叉点），树根编号为。现在这棵树的枝条太多了，需要剪枝，给定需要保留的树枝数量，求能留下多少苹果。

对于每个父节点的状态都是由它的子节点转移过来的，父节点上选择的边数完全取决于子节点的子树选择的边数。

令表示以为根节点的子树选择条边权值和最优解，

$f[u][i]=max(f[u][i],f[u][i-j-1]+f[v][j]+w)$

第一种策略，取以为父节点的条，的原因是如果要取这个子树，我们要取连接处（即的这一条）

第二种策略就是不取，代码如下：

void dfs (int p, int fath)
{
	for (int i = head[p]; il i = edge[i].nxt) // 前向星遍历 
	{
		int v = edge[i].to; // 取边的终点  
		if (v == fath) // 如果是子节点就返回  
			continue;
		dfs (v, p); // 向下递归  
		size[p] += size[v] + 1; // 子树边数在子节点子树的基础上加一，就是连结父子的边  
		for (int j = min (m, size[p]); j; j --)
		// j 到 1 是因为要留一条边连结父子，从还剩下的边数和本身子树边数里取最小值  
			for (int k = min (j - 1, size[v]); k >= 0; k --)
			// 首先是要留一条边所以 j - 1 ，然后就是能取的子树边数  
				f[p][j] = max (f[p][j], f[p][j - k - 1] + f[v][k] + edge[i].w);
	}
}

对于取最小值，大概就是瓶颈边（网络流里的叫法），一般来说是（总共取的边数）大，但是在这棵子树里是有限制的，但是取到后面子树边数甚至可能比总边数还多，这时候只能取剩余边数了，第二层循环边界同理，唯一要注意的点就是是为了取这棵子树，是个前提。

树上背包

~~这是最简单的动态规划问题。~~

树上背包问题，本质上是分组背包，比较经典的是《有线电视网》和《选课》。

选课

现在有门课程，第门课程的学分为，每门课程有零门或一门先修课，有先修课的课程需要先学完其先修课，才能学习该课程。

一位学生现在要学习门课程，求其能获得的最大学分。

每门课只有一门先修课的特点，与有根树里的父子关系相似。

因为有可能有一坨没有先修课的课程，所以形成了一坨森林，这个时候就可以增加一门编号为的学分的课程作为根（就可以当它是个虚点，但仍需存在）。

那么可以令表示第号点为根的子树里，已经遍历了号点的前棵树（这个地方可以看出分组背包的思想），选了门课程的最大学分。

转移的过程结合了树形和背包的特点，枚举父节点的每个子节点，同时枚举以为根的子树选了几门课程，将子树的结果合并到上。

记点的儿子数为（这门先修课下有多少门课），以为根的子树大小，就可以写出以下转移方程：

$f[p][j][k]=\max \lbrace f[p][j-1][k],f[v][s_v][l]+f[p][j-1][k-l]\rbrace$

代码如下：

void dfs (int p)
{
	for (int i = head[p]; ~i; i = edge[i].nxt)
	{
		int v = edge[i].to;
		dfs (v);
		for (int j = m + 1; j > 0; j ++) // m + 1 是因为要拿 0 编号课， j > 0 是因为要拿先修课  
		{
			for (int k = 0; k < j; k ++) // 可以拿从零节课拿起  
			{
				f[p][j] = max (f[p][j], f[p][j - k] + f[v][k]); // 和背包的代码差不多，取最优解
			}
		}
	}
}

有线电视网

某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构，这棵树的根结点位于足球比赛的现场，树叶为各个用户终端，其他中转站为该树的内部节点。

从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的，一场转播的总费用等于传输信号的费用总和。

现在每个用户都准备了一笔费用想观看这场精彩的足球比赛，有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。

找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。

实则也是就是个分组背包，换汤不换药。

对于这道题，有了前面的经验，状态和方程就更好推了，设表示以为根的子树，仅用前个儿子，满足个用户的最优解，方程如下：

$f[u][j]=\max\lbrace f[u][j],f[u][j-k]+f[v][k]-edge[k].w\rbrace$

代码如下：

int dfs (int u)
{
	if (u > n - m) // 用户终端边界
	{
		dp[u][1] = val[u];
		return 1;
	}
	int res = 0;
	for (int i = head[u]; i; i = edge[i].nxt)
	{
		int v = edge[i].to;
		t = dfs (v); // 因为是树所以肯定需要子树大小，也可以看做这一组的元素个数  
		sum += t;
		for (int j = sum; j >= 0; j --)
			for (int k = 1; i <= t; k ++)
				if (j - k >= 0)
					f[u][j] = max (f[u][j], f[u][j - k] + f[v][k] - edge[i].w)
	}
	return sum;
}

换根动态规划

~~这是最简单的动态规划问题。~~

当然有的时候问题需要的根是不定的，当然意思不是这个根会~~飘来飘去~~。

那我们最后来一道脚造例题好了：

移动城邦

泰拉大陆上的某个国家一共有个城市，每两个城市都互相可达（可能经过其他城市）。天灾即将来袭，需要在这些城市中选出一个中心城市来保护资源，现要求安排这个中心城市使得其他所有城市到它的距离和最大。

对于每个点都可以被当做根的这种问题，很显然，如果我们用的算法实在是……一言难尽，所以我们要设计出一种转移方法来减小到。

那其实就有一个很好的想法，从一个点转移到它的子节点，其贡献改变为其上面集体加这个点到子节点的距离和下面集体减这个点到子节点的距离，然后每个点的贡献直接通过公式转移就可以了。上面节点数就是下面节点数就是。

代码如下：

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int N = 4e5 + 1;

int n;

struct Edge {
	int nxt, to;
} edge[N];

int head[N], cnt;
int dis[N], siz[N], a[N], maxn, ans; 

inline void add_edge (int u, int v)
{
	edge[++ cnt].to = v;
	edge[cnt].nxt = head[u];
	head[u] = cnt;
}

priority_queue <pair <int, int> > Q;
bool vis[N];

void dijkstra (int s)
{
	memset (dis, 0x3f, sizeof dis);
	dis[s] = 0;
	Q.push (make_pair (0, s));
	while (!Q.empty ())
	{
		int x = Q.top ().second;
		Q.pop ();
		if (vis[x])
			continue;
		vis[x] = 1;
		for (int i = head[x]; i; i = edge[i].nxt)
		{
			int v = edge[i].to;
			if (dis[v] > dis[x] + 1)
			{
				dis[v] = dis[x] + 1;
				Q.push (make_pair (-dis[v], v));
			}
		}
	}
}

void dfs1 (int u, int fath)
{
	siz[u] = 1;
	for (int i = head[u]; i; i = edge[i].nxt)
	{
		int v = edge[i].to;
		if (v == fath) 
			continue;
		dfs1 (v, x);
		siz[u] += siz[v]; 
	}
}

void dfs2 (int u, int fath)
{
	for (int i = head[u]; i; i = edge[i].nxt)
	{
		int q = edge[i].to;
		if (q == fath)
			continue;
		a[q] = n + a[u] - 2 * siz[q];
		dfs2 (q, u);
	}
}

signed main ()
{
	int u, v;
	scanf ("%d", &n);
	for (int i = 1; i < n; i ++)
	{
		scanf ("%lld %lld", &u, &v);
		add_edge (u, v);
		add_edge (v, u);
	}
	dijkstra (1);
	for (int i = 1; i <= n; i ++)
		a[1] += dis[i]; 
	dfs1 (1, 0);
	dfs2 (1, 0);
	for (int i = 1; i <= n; i ++)
		if (a[i] > maxn)
			ans = i, maxn = a[i];
	printf ("%lld", ans);
}

边缘要赢到巨多例题！

基环树动态规划

~~这是最简单的动态规划问题。~~

基环树也叫环套树。

基环树听着很高大上，但是其实只不过是一个有个点个边的连通图，其性质是只有一个环并且删掉环上任意一条边都可以变成一棵树。

我是，基环树！

好像一个水母。

然后我们从一道例题开始讲这个（其实只有一道例题）。

卡西米尔骑士团

卡西米尔有很多骑士，比如锋盔骑士啦，呼啸骑士啦，左手骑士啦，杂七杂八的。

现在要组织一场比赛，有几个志同道合的骑士要组成一个骑士团打比赛。

但是有些骑士之间是有矛盾的，一个骑士不会和与自己有矛盾的人在同一个骑士团，现在要博士你组织一个骑士团去打比赛，使得这个骑士团内不出现有矛盾的两人（不存在骑士和与他痛恨的人一同被选入骑士团的情况），并且使得这个骑士团有战斗力，一个骑士团的战斗力为所有骑士的战斗力总和。

首先这个题目非常像《没有上司的舞会》。

虽然说里面有个环，但是我们可以将其拆开，然后从被拆开那条边的两个端点各自开始进行树形。

看一下完整代码，注释应该很详细了。

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int N = 1e6 + 1;

int n, m, a[N];

struct Edge {
	int nxt, to;
} edge[N << 1];

int head[N], cnt = -1; // 这里从 -1 开始

int f[N][2], ans, maxn; // 对于每个点选不选的状态  

int root1, root2, cut; // 对于环的连接边的编号和左右端点 

bool vis[N], cir[N];

inline void add_edge (int u, int v) // 前向星，不解释了 
{
	edge[++ cnt] = (Edge) {head[u], v};
	head[u] = cnt;
}

void find_circle (int p, int pre) // 找环  
{
	vis[p] = cir[p] = 1; // 标记访问和记录入环  
	for (int i = head[p]; i; i = edge[i].nxt)
	{
		int v = edge[i].to;
		if (cir[v] && i != (pre ^ 1)) // 入环且这条 p -> v 的边 i 不是前驱的反向边  
		{
			root1 = p; // 将其记录为两个根然后等等进行树形dp 
			root2 = v;
			cut = i; // 记录被拆开的边的编号   
		}
		if (!vis[v])
			find_circle (v, i); // 对于一个还未访问的点那就继续访问 
	}
	cir[p] = 0; // 回溯，取消入环记录 
}

void dfs (int p, int pre)
{
	f[p][0] = f[p][1] = 0;
	for (int i = head[p]; i; i = edge[i].nxt)
	{
		int v = edge[i].to;
		if (v == pre || i == cut || i == (cut ^ 1)) // 要不到头，要不就是这个边是连接边 
			continue;
		dfs (v, p); // 向下递归 
		f[p][1] += f[v][0]; // 具体详见 《没有上司的舞会》，前面应该有讲  
		f[p][0] += max (f[v][1], f[v][0]); 
	}
	f[p][1] += a[p]; // dfs 完统计自己的答案 （诶这个时候是自己要选的哟） 
}

signed main () 
{
	scanf ("%lld", &n);
	for (int i = 1, x; i <= n; i ++)
	{
		scanf ("%lld %lld", &a[i], &x);
		add_edge (i, x);
		add_edge (x, i); // 这里选用无向图 
	}
	for (int i = 1; i <= n; i ++)
		if (!vis[i])
		{
			maxn = 0;
			find_circle (i, -1);
			dfs (root1, 0); // 从一个端点开始 dfs  
			maxn = max (f[root1][0], maxn); // 这边其实就是肯定有一个端点是不能用嘀！
			dfs (root2, 0); // 从另一个端点开始 dfs  
			maxn = max (f[root2][0], maxn); // "
			ans += maxn;
		}
	return printf ("%lld", ans) & 0;
}

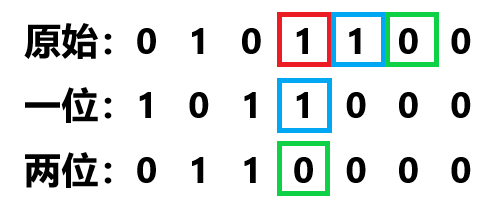
状态压缩动态规划

~~这是最简单的动态规划问题。~~

状压，是利用计算机二进制的性质来描述状态来达到优化转移的一种方式。

：始开目题的谈常生老个一从们我让

炮兵阵地

司令部的将军们在的网格地图部署炮兵部队，一个地图由两种地形组成，用来表示山地，用来表示平原，其中山地不可以部署炮兵部队。

在每一个平原地形上最多可以部署一支炮兵部队，一支炮兵部队的攻击范围是这样的：

现在，将军们该如何部署炮兵部队，在防止误伤的情况下，最多能摆放多少支炮兵部队。

现在有一个很好的想法，我可以利用一个串来表示每个位置放不放炮兵，表示放，表示不放，那么就有行，效果如下：

$\large 1\ \ \ \ \ 0\ \ \ \ \ 0\ \ \ \ \ 1\ \ \ \ \ 0\ \ \ \ \ 0\ \ \ \ \ 1$

如果这是其中一行的状况，可以将其表示为一个整数，也就是把这个串转化为十进制数：

$73=1+8+64= 1 \times 2^0 + 1 \times 2^3 + 1 \times 2^6$

我们就可以令表示第行，的状况时的最优解，但是这题不太一样，需要考虑到旁边两条条的情况，所以我们增加一维状态，其中表示当前枚举第行，表示当前行的状态，表示上一行的状态。

对于左右呢，我们要请出位运算！

$\large 0\ \ \ \ \ 1\ \ \ \ \ 0\ \ \ \ \ 1\ \ \ \ \ 1\ \ \ \ \ 0\ \ \ \ \ 0$

对于这样一行状态，考虑到可以使用位运算 & ，即“与”，存在 & ， & 和 & ，当同时为真结果才为真。

那么我们就可以对这个串进行左移 << 和右移 >> ，来简单地判断左右放的炮兵是否冲突，左移一位（判断右边）是否效果如下：

左移的情况非常的有意思

然后对比这一列发现右边有一个是冲突的（好吧这是显而易见的），右移就是对比左边的。

判断上下的时候就很简单，直接比对这两行有无冲突就好了：

呐你看这就很简单了

转移方程就是如果满足这两个前提就加上这一排最多能放的就是了：

$f[i][j][k_1]=\max\lbrace f[i][j][k_1],f[i-1][k_1][k_2]+val[j]\rbrace$

也许完整的代码如下：

#include <bits/stdc++.h>

using namespace std;

int n, m, F[105], f[105][66][66], start[70], cnt = 0, val[200];
bool mp[105][30];

int main ()
{
	char ch;
	scanf ("%d %d", &n, &m);
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= m; j ++)
		{
			cin >> ch;
			if (ch == 'H')
				mp[i][j] = 1;
		}
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= m; j ++)
			F[i] = (F[i] << 1) + mp[i][j];
	start[++ cnt] = 0;
	for (int i = 1; i < (1 << m); i ++)
	{
		if (i & (i << 1))
			continue;
		if (i & (i << 2))
			continue;
		if (i & (i >> 1))
			continue;
		if (i & (i >> 2))
			continue;
		start[++ cnt] = i; // 存有价值的  
		int x = i;
		while (x) // 求每个状态的贡献  
		{
			val[cnt] ++;
			x -= (x & (-x));
		}
	}
	for (int i = 1; i <= cnt; i ++) 
		if ((start[i] & F[1]) == 0)
			f[1][i][0] = val[i];
	for (int i = 1; i <= cnt; i ++)
		if ((start[i] & F[2]) == 0)
			for (int j = 1; j <= cnt; j ++)
				if ((start[i] & start[j]) == 0 && (start[j] & F[1]) == 0)
					f[2][i][j] = val[i] + val[j];
	for (int i = 3; i <= n; i ++)		
		for (int j = 1; j <= cnt; j ++)	// 当前一排状态		
			if ((start[j] & F[i]) == 0)
				for (int k1 = 1; k1 <= cnt; k1 ++) // 上面第一排			
					if ((start[j] & start[k1]) == 0 && (start[k1] & F[i - 1]) == 0)					
						for (int k2 = 1; k2 <= cnt; k2 ++) // 上面第二排				
							if ((start[j] & start[k2]) == 0 && (start[k1] & start[k2]) == 0 && (start[k2] & F[i - 2])==0)
								f[i][j][k1] = max (f[i][j][k1], f[i - 1][k1][k2] + val[j]);
	int ans = 0;
	for (int i = 1; i <= cnt; i ++)
		for (int j = 1; j <= cnt; j ++)
			ans = max (ans, f[n][i][j]);
	return cout << ans, 0;
}

对于一坨题目，推荐这个博客：偷学笔记，讲的非常多，非常棒！

数位动态规划

~~这是最简单的动态规划问题。~~

数位常用于计数问题，一般来说是统计某个区间中满足某个条件的整数的个数，可以想到有一种朴素的方法来统计：

bool f (int x)
{
	cnt = 0;
	while (x) // 分解数位 
	{
		a[cnt ++] = x % 10;
		x /= 10;
	}
	reverse (a, a + cnt); // 也可以不调换位置，看个人喜好 
}
for (int i = l; i <= r; i ++)
	if (f (i) == true)
		ans ++;

但是这样时间复杂度是的，非常糟糕，而且都不方便记忆化，那甲方肯定是不能接受的，所以我们要使用数位了！

数位通常使用记忆化搜索的方式来实现。例如我们要求以内符合条件的数，我们只要知道形如、或，且小于等于原数的符合条件的数的数量即可。

让我们用一道早死偶缄的的题目开始：

数字计数

给定两个正整数和，求在中的所有整数中，每种数码（）出现了多少次。

数位和其他很多一样，减少复杂度的核心就是合并相同状态，有些答案是一样的，那么就可以当做相同的状态，当枚举到的时候发现这种状态的答案已经被记录过了，于是可以直接返回。

还有一个很有意思的新东西就是，决定这一位枚举啥数字的状态，表示当前位最多能取到原数这一位的数，还是可以任意取 ~ ，比如现在原数是，此时分两种情况：

如果此时是百位是，那么十位就可以取和：

示意数字已不见踪影

因为这个时候十位的数不能大于百位的数（好像是句废话？）：

少女填数中……

但是如果此时百位的数是，十位怎么填都不能大于原数，所以可以随便填：

少女乱填中……

至于前导零，看运气，看你遇到的啥题目，~~面对题目编程~~。

一般来说的话，前面位数枚举零就算作是枚举位数比原数少的数。

然后采用前缀和思想算区间的解，在主函数里这么调用：

1	printf ("%d", f (r) - f (l - 1));

完整代码如下（缝合拼接怪，我把两份完全不一样的代码拼到了一起）：

#include <bits/stdc++.h>
#define int long long

using namespace std;

int A[21], cnt, digit, f[22][22][2][2];

int dfs (int pos, int cntd, bool limit, bool lead)
// pos 当前位置， cntd 目前为止找到了多少个数码， limit 表示上界， lead 表示是否为 0 (true 为 0) 
{
	int ans = 0;
	if (pos == 0) // 边界 
		return cntd; // 返回个数 
	if (f[pos][cntd][limit][lead] != -1) // 如果被记忆化过了，就直接返回  
		return f[pos][cntd][limit][lead];
	for (int v = 0; v <= (limit ? A[pos] : 9); v ++) 
	// 如果 limit 为假，则 0 ~ 9 
		if (lead && v == 0) // 前一位是 0 而且它是 0 
			ans += dfs (pos - 1, cntd, limit && v == A[pos], true); 
			// pos - 1 向下推， cntd 因为是前导零所以不增加， limit 随着 v 是否等于 A[pos] 而改变，这一位是零 
		else  // 这一位挺正常的  
			ans += dfs (pos - 1, cntd + (v == digit), limit && v == A[pos], false);
			// pos - 1 同上， cntd 增加当前答案， limit 同上，这一位不是前导零
	f[pos][cntd][limit][lead] = ans; // 记忆化 
	return ans; 
}
int calc (int x) // 将原数分成数位
{
	cnt = 0;
	memset (f, -1, sizeof (f));
	memset (A, 0, sizeof (A));
	while (x) // 解剖结果出来了，死亡原因是解剖  
	{
		A[++ cnt] = x % 10; // 总之就是一位一位拿下来  
		x /= 10;
	}
	return dfs (cnt, 0, true, true); 
	// 这是从高位到低位，如果是从低位到高位，要把上面的 pos - 1 改成 pos + 1 ，因为枚举长度是向上的，同样改变边界为 cnt 
}

signed main ()
{
	int a, b;
	scanf ("%lld %lld", &a, &b);
	for (int i = 0; i < 10; i ++)
	{
		digit = i; // 说明一下这次我们要找谁  
		printf ("%lld ", calc (b) - calc (a - 1));
	}
	return 0;
}

期望动态规划

数学期望

~~这是最简单的……这好像也不是动态规划问题啊……~~

对于一组离散型变量，出现其中某一变量的概率乘以这一变量值，求和，就是数学期望，如下：

$E=\sum^n_{i=1}(p_i\times v_i)$

所谓期望，其实表示的是一组离散型随机变量的平均水平，也就是进行某件事能得到的平均结果，或理想代价。

就好像我买次彩票，中彩票的概率为，中的次数是，边缘抽中一次彩票的期望就是。

也好像我打次模拟赛，程序全挂的概率为，全挂的次数是，那么模拟赛全挂的期望就是。

期望DP

~~这是最简单的动态规划问题。~~

对于一种很难找到递推关系的数学期望问题，就可以利用期望的定义式，根据实际情况，以概率或方案数（或它们的乘积）表示一种状态，一般来说还是用来表示遍历到第件事的期望。

求我现在会用老生常谈的题目开始的期望：

麻球繁衍

一开始有个麻球，每个麻球只能活一天，翘辫子的时候有的概率产生只麻球（也只能活一天），求天内所有麻球都翘辫子的期望。

首先，可以想到，如果中一张彩票概率是，那么中两张彩票的概率就是（好吧其实两者都是）。

那么以此类推，考虑一只麻球在天后去掉了的概率是，那么两只麻球在天死亡的概率就是。

考虑一只麻球，结合全概率公式，天全部翘辫子的概率为：

$f[i]=p_0+p_1f[i-1]+p_2f[i-2]^2+...+p_{n-1}f[i-1]^{n-1}$

那么答案就是，表示只麻球在天后同时翘辫子的期望。

代码如下：

#include <bits/stdc++.h>

using namespace std;

const int N = 1e3 + 1;
int k, n, m, t;
double p[N], f[N];

int main ()
{
	scanf ("%d", &t);
	for (int tt = 1; tt <= t; tt ++)
	{
		memset (f, 0, sizeof (f));
		memset (p, 0, sizeof (p));
		scanf ("%d %d %d", &n, &k, &m);
		for (int i = 0; i < n; i ++)
			scanf ("%lf", &p[i]);
		f[1] = p[0];
		f[0] = 0;
		for (int i = 2; i <= m; i ++)
		{
			f[i] = 0;
			for (int j = 0; j < n; j ++)
				f[i] += p[j] * pow (f[i - 1], j);
		}
		printf ("Case #%d: %.7lf\n", tt, pow (f[m], k));
	}
	return 0;
}

原题题目名是，在阿斯图里亚斯语里的意思是四叶草，而且麻球好像是一种吃的……不是小鸟吧……（不是很懂为什么叫麻球 www ）

插头动态规划

~~这是最简单的动态规划问题。~~

插播一个喜报：前一天准备要写的时候我在听相声《华容道》，然后这个时候临近晚自修下课了，突然教授的桌子下出现了蟑螂哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈，教授第一次看到还在叫我，然后不见了，第二次在他的脚下出现了，他吓得整个人直接弹开哈哈哈哈哈哈哈哈哈哈哈哈哈哈，然后蟑螂就不见了，教授，你弹开的样子真的很狼狈。

然后我还在宿舍里和他说，你就不能把蟑螂看做吗哈哈哈哈哈哈哈哈哈哈，他说他第一次见活的蟑螂哈哈哈哈哈哈哈哈哈哈哈不行了头都要笑掉了。

美洲大蠊

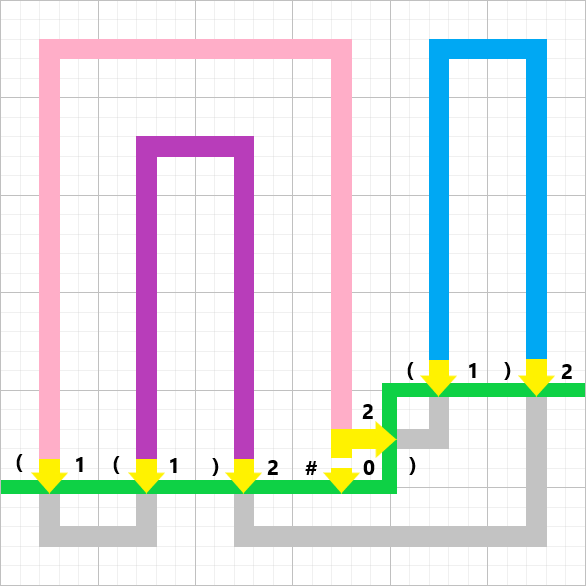
插头动态规划问题是一种基于连通性的动态规划问题，我们从一道 $** $ 的题来讲：

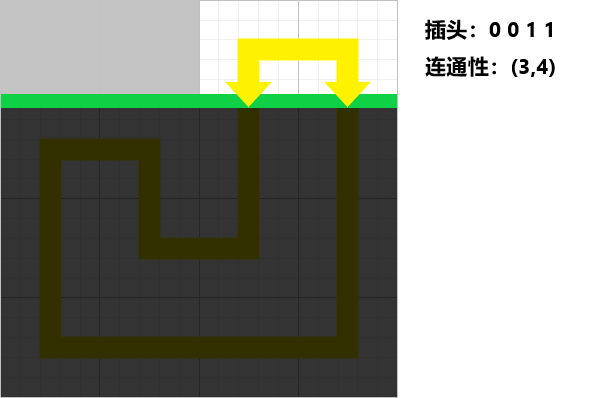
插头

给出的方格，有些鸽子有障碍，不能铺线，其他鸽子必须铺，形成一个闭合回路。问有多少种铺法。

其实应该叫轮廓线动态规划，这个之后会讲，反正我知道大家肯定都懂了（悲）。

那还是来给个例子，比如以下的情况：

这个图可难搞

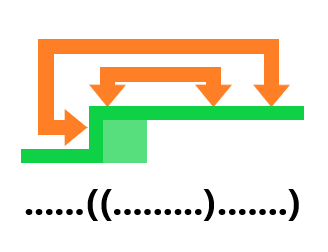
插头

对于一个四连通的问题来说，它通常有上下左右四个插头，一个方向的插头存在表示这个格子在这个方向可以与外面相连。

可以发现所有的非障碍格子一定是从一个格子进来，另一个格子出去，即四个插头恰好有两个插头存在，共六种情况。

有四个方向

然后那么存在六种情况：

略，这个图也很难画，最后一个的灰色多了一条来补

然后我们要做的就是用这些“拼图”形成一个回路，就很像接水管游戏。

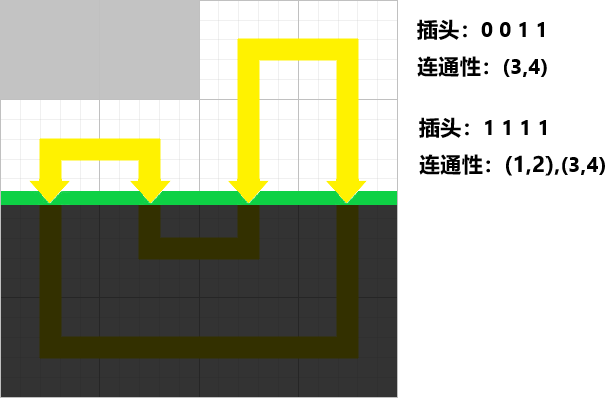
轮廓线

相信大家都听说过，轮廓线就是当前决策的边界，即已决策鸽子和未决策鸽子的界线：

不可决策界线

轮廓线上方与其相连的最多有个插头位置，包括个下插头和个右插头，这是逐格递推，按照从上到下，从左到右的顺序考虑每一格。

地生五煌

还有一种是逐行递推，从上到下的顺序依次考虑每行：

这个方法基本不会用

状态

逐行递推的状态

不妨按照从上到下的顺序依次考虑每一行，分析第行的哪些信息对第行有影响。

我们需要记录第行的每个格子是否有下插头，这决定了第行的每个格子是否有上插头。

但是仅仅记录插头是否存在是不够的，可能导致出现多个回路，而本题仅要求一个回路。

比如可能会出现这种诡异的情况

也就隐含着最后所有的非障碍格子通过插头连接成了一个连通块，因此还要记录第行的个格子的连通情况。

那么让我们来模拟一下：

第一行！

因为左边的两个格子是障碍，所以没有下插头，第格和第格通过上面的插头是连通的。

第二行！

四个格子都有下插头，第格和第格相连通，第格和第格相连通。

现在大家都连通啦

中间的两格不存在下插头，这四格通过弯弯曲曲的回路相连。

通过上面的分析，可以写出动态规划的状态。用表示前行，第行的个格子是否具有下插头的一个位的二进制数为，第行的个格子之间的连通性为的方案总数。

关于连通性，我们通常给每一个格子标记一个正数，属于同一个的连通块的格子标记相同的数，比如和都表示第个格子属于一个连通块，第个格子属于一个连通块，为了避免出现同一个连通信息有不同的表示，一般会使用最小表示法。

最小表示法为所有的障碍格子标记为，第一个非障碍格子以及和它连通的所有格子标记为，然后再找第一个未标记的非障碍格子以及与它连通的格子标记为，重复这个过程直到所有格子都被标记（说实话有点像染色）。

比如连通信息表示为，对于格子标为，对于标为，对于遗留下来的标为，当然还有别的方法，这里不多赘述。

我们就可以拿出之前的那个例子来试手。

对于第一行，前两格因为是障碍所以是，后面两格有插头且连通：

似曾相识

对于第二行，全都有下插头，前两格相连，后两格相连

似曾相识

对于第三行，前后两格有下插头，中间四格全都相连，属于一个连通块：

****（被禁言了）

插播一个喜报：夏天晚霞超级好看！！！

通过观察发现如果轮廓线上方的个格子中的某个格子没有下插头，那么它就不会再与轮廓线以下的格子直接相连，它的连通性对轮廓线一下的格子不会再有影响，也就成为了冗余信息，所以可以将记录格子连通性改成记录插头的连通性。如果这个插头存在，那么就标记这个插头对应的格子的连通标号；如果这个插头不存在，那么标记为，这样就可以把状态从精简为。

比如之前的第三行的状态：

$f(3,(1001)_2,\lbrace1,1,1,1\rbrace)$

就可以表示为：

$f(3,\lbrace1,0,0,1\rbrace)$

同理，第二行的是这样的：

$f(2,(1111)_2,\lbrace1,1,2,2\rbrace)\rightarrow f(2,\lbrace1,1,2,2\rbrace)$

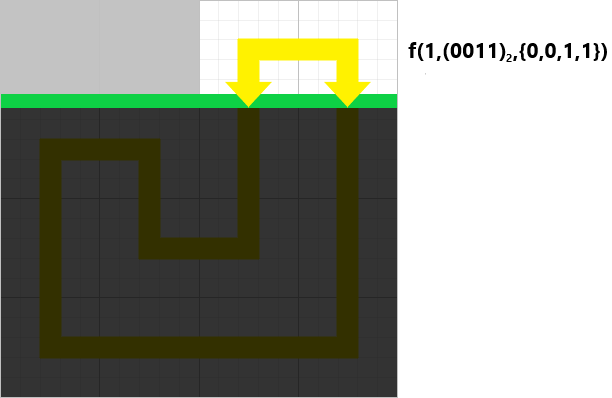
逐格递推的状态

因为逐行递推很慢，所以要来讲逐格递推。

从左到右依次给个格子标号，个插头标号类似地，我们需要记录与轮廓线直接相连的个插头是否存在以及个格子的连通情况。

表示当前转移完这个格子，个插头是否存在表示成一个位的二进制数，以及个格子的连通性为的方案总数。

当然也可以类似优化，格子的连通性记录在插头上，状态变为。

来做个模拟！给一些大家肯定都看到过的图（哦我之前放过了，那比较尴尬）。

对于第一格，有一个存在的下插头和一个不存在的右插头。

所以此时的状态为：

$f(3,1,\lbrace1,0,1,2,2\rbrace)$

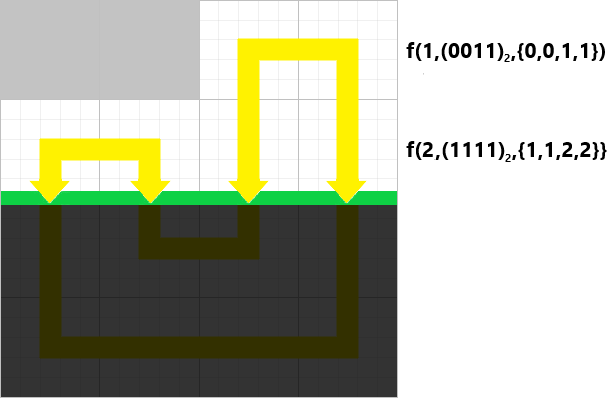
对于第二格，有一个存在的右插头和一个不存在的下插头，然后左右的连通块不相连：

所以此时状态为：

$f(3,2,\lbrace1,0,1,2,2\rbrace)$

对于第三格，有一个不存在的下插头和一个不存在右插头，然后两边全部连通：

例例例

所以此时状态为：

$f(3,3,\lbrace1,0,0,0,1\rbrace)$

简单的回路问题

对于简单的回路问题，我们可以找出两个特点。

插头两两匹配，可以从下面这张图发现这个特点：

发现什么了嘛

可以发现轮廓线上方是由若干条互不相交的路径构成的，而每条路径的两个端口恰好对应了轮廓线上的两个插头。

一条路径上的所有格子对应的是一个连通块，而每条路径的两个端口对应的插头是连通的，而且不与其他任何一个插头连通。

插头不会交叉，设现在轮廓线上从左到右四个插头，，，，如果与相连，并且与不连通，那么和一定不连通。

诶你看完全不会交叉

由此我们可以找出存储插头状态的方法，就是括号序列。

括号表示法

我们可以用这种法则来表示插头连通性：

是活的三进制！

给出上面那个图的例子：

图……好……大……

那么可以写成：

用MathJax好像会炸，于是就改成图片了

用三进制表示为：

$(1120212)_3$

可能图会比较糊，但是我们要讲接下来的了。

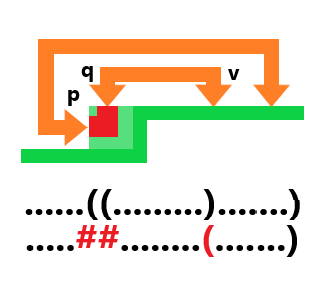
转移状态

逐行递推

假设从第行转移到第行，我们需要从左到右枚举的每个格子的状态（共六种情况）。对于任何一个非障碍格子，它是否有上插头和左插头已知（因为和上面那一行有关系），因此最多只有两种情况，状态的转移数。

对于左边和上边有插头的情况，格子的状态是一定确定的：

咦……现在才发现这个图好小

然后对于上面有插头的情况，有两种情况，第一种是直下：

真的好小

还有一种是向右弯：

诶那你可能就会疑惑

至于这里为什么没有向左弯，是因为必须存在两个插头才可以确定，因为你是从左边推过来的，如果是左边那一格的没有插头呢，对吧，一定要保证左边的是右插头才能确定这一格的状态为向右弯。

然后对于左边有插头的情况，也有两种情况，第一种是直左：

像……金箍棒

同上面，还有一种是向下弯，理由前面说过了，这里不再赘述：

这个时候应该就没有疑惑了

最后一种情况是肯定的，因为这是在没有插头的情况下：

你看根本就没有出现插头对吧

枚举完第行每个格子的状态后，需要计算第行个格子之间的联通性。通常可以使用并查集的数组来对其重新标号，或者重新执行一次搜索，时间复杂度为，最后将格子的联通性转移到插头的连通性上。

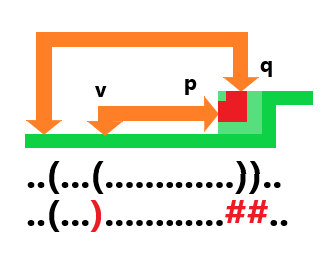
逐格递推

然后关键其实是逐格递推。

为了表述方便，设当前转移格，格右插头是，是下插头，格的右插头和下插头分别是和。

那么每次转移相当于轮廓线上插头的信息修改成的信息，插头的信息修改成，设表示插头的状态。

如果你没有听懂这个关于修改的事，没有关系，这个时候就要开始分类讨论了，分类讨论的时候你应该就能听懂了。

第一种情况

新建一个连通分量，也就是我们之前说的这个：

我不允许你对我连通的分量大放厥词

那么这个的情况下，，和两个插头构建了一条新的路径，相当于为左括号，为右括号，

即：

$p'\leftarrow1,q'\leftarrow2$

计算新的状态的时间为，然后我们来举个例子：

诶嘿一种新的方式！

在转移这一格之前，轮廓线应该是：

这样滴

然后我们转移：

这个时候轮廓线就是：

那样滴！

轮廓线第二个和第三个状态被改变了。

第二种情况

接下来是合并两个连通分量，也就是我们说的：

很有设计感，真的

这种情况下，反正就是左边和上面不至于没有插头，那么对应的：

$p'\leftarrow0,q'\leftarrow0$

接着根据为左括号还是右括号分四类情况讨论，接下来靠图辨认吧。

第一种情况，要连接的两个是左括号。

原本是这样的：

现在变成了这样：

或者未来

就是把左边这俩连起来，那么轮廓线就进化了，这个的话用栈来维护就好。

$w(p)=1,w(q)=1$

那么需要将这个左括号与之对应的右括号修改成左括号，即。

时间复杂度是还算不错的。

第二种情况，要连接的是两个右括号。

直接放图了，大家肯定都看的懂，看不懂我也没有办法：

我觉得……这个图……好像一只乌龟……啊

把右边这俩连起来就能把那俩扭曲的右括号变成俩不扭曲的井号。

$w(p)=2,w(q)=2$

那么需要将这个右括号与之对应的左括号修改成右括号，即。

时间复杂度是还算**的。

第三种情况，接上了对应的左括号和右括号。

那么显然这种情况只能出现在最后的时候，不然就会出现回路错误。

你看，这不就结束了（结束了吗？）

能把这最右边的这俩括号变成井号。

$w(p)=1,w(q)=2$

那么和是相对应的左括号和右括号，连结起来相当于将一条路径的两端连接起来形成一个回路，这种情况下只能出现在最后一个非障碍格子。

时间复杂度是非常不错的。

第四种情况，接上不对应的左括号和右括号。

这种就没有关系哩！来看图~

其实没有结束哦

能把中间这俩背靠背的括号变成井号。

$w(p)=2,w(q)=1$

那么连结起来后对应的左括号和对应的右括号恰好匹配，不需要修改其他插头的状态，只有这俩插头修改的世界完成了~

时间复杂度为非常**的。

第三种情况

你可能以为是总共有六个，但是其实只有三个。

所以是事倍功半。

啊不对是事半功倍。

啊呀随便吧。

你以为我会说三句废话。

其实只要断一断。

就可以说——（啪）。

其实这里是剩下的四个插头，因为它们都是保持原来的连通分量，即中恰好一个为，因此也恰好一个为。

那么无论中的哪个插头存在，都相当于是中那个存在插头的延续，括号性质一样，因此有：

$w(p')\leftarrow w(p)+w(q),w(q')\leftarrow0$ $w(q')\leftarrow w(p)+w(q),w(p')\leftarrow0$

计算新的状态的时间复杂度为。

比如这个情况：

就是这么填，不填拉倒

然后这个应该是这样的括号序列：

只有我做的图片，凋零在博客里面~

那你总不可能这么填吧：

诶就说不定呢

那这个又是这样的括号序列了：

插头微凉，图片微凉~

小型总结水晶

括号表示法和最小表示法是差不多的，但是除了第三种情况，每一次转移都要重新扫描。

逐行递推的每一个转移的状态总数为指数级，而逐格递推是的。

每次计算新的状态的时间两者最坏情况都是的。但是逐行递推的常数要比逐格递推大，从转移开销这个角度来看，逐格递推的优势是毋庸置疑的，所以大部分情况下都用逐格递推。

哈希表的食用

~~诶是不是以为自己翻错博客了。~~

这么多状态，其实很多状态是无效重复的，所以可以建立一个哈希表进行记忆化，采用记忆化宽度优先搜索。

状态为，可以使用一个比较小的哈希表，每转移一个清空一次。

其实呢，每次判断状态是否扩展过的程序效率比用一个较大的的哈希表每次判断状态高很多。

类似地，在不需要记录路径的情况下，也可以使用滚动的扩展队列来代替一个大的扩展队列。

代码

咕咕咕，现在我的模板题只能拿二十分……等我再调一调（估计到暑假前是调不出来了）。

但是下面是参考代码：

#include <bits/stdc++.h>

using namespace std;

const int N = 14;
const int mod = 4001;

int n, m, endx, endy;

int now, last;

long long ans;

bool a[N][N];

int head[mod + 5], nxt[2 << 24], que[2][2 << 24], cnt[2], inc[N];

long long val[2][2 << 24];

char s[101];

inline void init ()
{
	scanf ("%d %d", &n, &m);
	for (int i = 1; i <= n; i ++)
	{
		scanf ("%s", s + 1);
		for (int j = 1; j <= m; j ++)
			if (s[j] == '.')
			{
				a[i][j] = 1;
				endx = i;
				endy = j;
			}
	}	
	inc[0] = 1;
	for (int i = 1; i <= 13; i ++)
		inc[i] = inc[i - 1] << 2; 
}

inline void insert (int bit, long long num)
{
	int u = bit % mod + 1;
	for (int i = head[u]; i; i = nxt[i])
		if (que[now][i] == bit)
		{
			val[now][i] += num;
			return ;
		}
	nxt[++ cnt[now]] = head[u]; // 这里采用挂表法  
	head[u] = cnt[now]; // 诶是不是和前向星很像  
	que[now][cnt[now]] = bit;
	val[now][cnt[now]] = num;
}

inline void work ()
{
	cnt[now] = 1; // hash 末指针  
	val[now][1] = 1; // 记录状态值 
	que[now][1] = 0; // 队列记录状态
	for (int i = 1; i <= n; i ++)
	{
		for (int j = 1; j <= cnt[now]; j ++)
			que[now][j] <<= 2;
		// 到每行第一个格子时在前面补一个空插头，剩下的部分从上一行最后一个格子那里直接搬过来
		for (int j = 1; j <= m; j ++)
		{
			memset (head, 0, sizeof (head)); // 清空 hash 
			last = now;
			now ^= 1;
			cnt[now] = 0; // 清空 hash
			for (int k = 1; k <= cnt[last]; k ++) // 枚举所有状态 
			{
				long long bit = que[last][k], num = val[last][k]; // 获取当前状态
				int p = (bit >> ((j - 1) * 2)) % 4, q = (bit >> (j * 2)) % 4;
				if (!a[i][j]) // 当前点有障碍 
					if (!p && !q)
						insert (bit, num);
				else if (!p && !q) // 无右插头，无下插头 
					if (a[i + 1][j] && a[i][j + 1]) // 左，上无障碍 
						insert (bit + inc[j - 1] + (inc[j] << 1), num); // 添加一个连通分量 
				else if (!p && q) // 无右插头，有下插头，情况三 
				{
					if (a[i][j + 1]) // 左无障碍  
						insert (bit, num);
					if (a[i + 1][j]) // 上无障碍  
						insert (bit - inc[j] * q + inc[j - 1] * q, num);
				}
				else if (p && !q) // 有右插头，无下插头，情况三  
				{
					if (a[i + 1][j]) // 上无障碍 
						insert (bit, num);
					if (a[i][j + 1]) // 左无障碍 
						insert (bit - inc[j - 1] * p + inc[j] * p, num);
				}
				// 有右插头，有下插头，情况二 
				else if (p == 1 && q == 1) // 情况 2 - 1 
				{
					int k1 = 1;
					for (int l = j + 1; l <= m; l ++)
					{
						if ((bit >> (l * 2)) % 4 == 1)
							k1 ++;
						if ((bit >> (l * 2)) % 4 == 2)
							k1 --;
						if (!k1)
						{
							insert (bit - inc[j] - inc[j - 1] - inc[l], num);
							break;
						}
					}
				}
				else if (p == 2 && q == 2) // 情况 2 - 2 
				{
					int k1 = 1;
					for (int l = j - 2; l >= 0; l --)
					{
						if ((bit >> (l * 2)) % 4 == 1)
							k1 --;
						if ((bit >> (l * 2)) % 4 == 2)
							k1 ++;
						if (!k1)
						{
							insert (bit - (inc[j] << 1) - (inc[j - 1] << 1) + inc[l], num);
							break;
						}
					}
				}
				else if (p == 2 && q == 1) // 情况 2 - 4
					insert (bit - (inc[j - 1] << 1) - inc[j], num);
				else if (i == endx && j == endy) // 情况 2 - 3
					ans += num; 
			} 
		}
	}
}

int main ()
{
	init ();
	work ();
	printf ("%lld", ans);
}

动态规划优化

单调队列优化

~~这是最简单的动态……优化！~~

就是用单调队列来优化，这里给出例题：

制造站

基建里有个排成一排的制造站，现在博士要安排干员搓赤金，每个制造站里有一个干员，每个干员的效率是不同的，干员的效率是。

相邻制造站里的干员是互相熟悉的，如果博士安排超过连续个制造站搓赤金，那么这些干员就会罢工，在宿舍里开派对，现在求博士能得到的最大效率。

那我们可以设计状态，对于这种一排的元素，可以设计对于每个元素选或不选，所以设为以结尾，并且不选所得到的最大效率值；相反，设为以结尾但是选的最大效率值。

然后为了方便可以预处理出一个前缀和，由此我们得到一个转移方程：

$\begin{aligned}{} f[i][0]&=\max(f[i-1][0],f[i-1][1])\\\\ f[i][1]&=\max(f[x][0]-s[x])+s[i] \ \ \ \ (i-m\leq x\leq i)\\\\ \end{aligned}$

发现可以用单调队列优化，维护队首为最大的单调队列。

代码给出：

int l = 1, r = 1;
for (int i = 1; i <= n; i ++)
{
	f[i][0] = max (f[i - 1][0], f[i - 1][1]);
	while (q[l] < i - k && l <= r)
		l ++; // 维护队首 
	f[i][1] = f[q[l]][0] - sum[q[l]] + sum[i]; // 这样就可以得到当前最佳答案了！ 
	while (f[i][0] - sum[i] > f[q[r]][0] - sum[q[r]] && l <= r)
		r --; // 维护队尾
	q[++ r] = i; // 入队
}
printf ("%d", max (f[n][0], f[n][1]));

主要还是为了方便。

决策单调性优化

~~这是最简单的动态规划劣化。~~

决策单调性是在最优化 中的可能出现的一种性质，利用它我们可以降低转移的复杂度。

对于形如的式子，设从这个位置转移，如果。那么这个就满足决策单调性。

要做的就是为每个决策点分配对应的决策区间。

四边形不等式

四边形不等式的定义是：

如果对于：

$\forall a_1 \leq a_2 < b_1 \leq b_2$

存在：

$m[a_1][b_1]+m[a_2][b_2]\leq m[a_1][b_2]+m[a_2][b_1]$

则满足四边形不等式。

对于一个区间值关系，如果它满足交叉小于包含，就说明它满足四边形不等式。

有一说一，上面那个东西也叫蒙日阵，这个东西我们之后会提到。

但是只能用在最小值上，结论如下（别问我我也不知道）：

$s[i][j-1]\leq s[i][j]\leq s[i+1][j]$

在查找最优分割点的时候，我们浪费了大量时间，那么我们可以把最优分割点保存下来，在查找的时候利用保存的最优分割点来优化查找过程，模板代码如下：

for (int i = 1; i <= n; i ++) // 预处理
{
	sum[i] = sum[i - 1] + w[i];
	sum[i + n] = sum[i + n - 1] + w[i];
	relation[i][i] = i;
	relation[i + n][i + n] = i;
	f[i][i] = 0;
	f[i + n][i + n] = 0;
}
for (int i = 1; i <= n; i ++) // 枚举长度  
{
	for (int j = 1; i + j <= 2 * n; j ++) // 区间左端点  
	{
	 	int end = i + j - 1; // 区间右端点  
		for (int k = relation[j][end - 1]; k < relation[j + 1][end]; k ++) 
		{
			if (f[j][end] > dp[j][k] + f[k + 1][end] + sum[end] - sum[j - 1])
			{
				f[j][end] = dp[j][k] + dp[k + 1][end] + sum[end] - sum[j - 1];
				relation[j][end] = k;
			}
		}
	}
}

二分栈

给出一道老生常谈的题目：

玩具装箱

教授要去看美女，但是他舍不下自己的玩具，于是他决定带上自己所有的玩具。他使用自己的压缩器进行压缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。

教授有编号为的件玩具，第件玩具经过压缩后的一维长度为。

为了方便整理，教授要求，在一个一维容器里的玩具编号是连续的；同时如果一个一维容器中有多个容器，那么两件玩具之间要加入一个单位长度的填充物，形式地说，如果将第件玩具到第件玩具放到一个容器中，那么容器的长度将为。

制作容器的费用与容器的长度有关，根据教授研究，如果容器长度为，其制作费用为。其中是一个常量。（棘手）不关心容器的数目，他可以制作出任意长度的容器，甚至超过。但他希望所有容器的总费用最小，因为他很强所以他可以自己写一个程序来解决这个问题。

首先其实状态是很好设的，可以设为前个玩具装完之后所需要的最小花费，转移方程如下：

$f[i]=\min\lbrace f[j]+(sum[i]-sum[j]+i-j-1-L)^2|0\leq j<i\rbrace$ $sum=\sum_{j=1}^ic[j]$

此处我们要证明这是一个可以用单调决策性的题目，我们就要看看这个东西七搞八搞以后能不能符合四边形不等式，考场上就代几个数字进去看看就好了，只要你不是那种运气特别差的基本都能~~证出来~~，不多说，我们开证：

先设，则我们可以拓展出三个看不懂的东西：

为了方便，我们设，则：

$w(i+1,j+1)=(x+c[i+1]-c[j+1])^2$ $w(i+1,j)=(x+c[i+1]+1)^2$ $w(i,j+1)=(x-c[j+1]-1)^2$

最终可以化出这么个东西：

$w(i,j)+w(i+1,j+1)\leq w(i+1,j)+w(i,j+1)$

是不是似曾相识。

然后我们可以用一个栈维护每个决策的起始和结束位置。对于每个已经计算出的，去寻找它能更新的状态有哪些。

在栈顶的决策起始位置判断起始位置来判决策是否更优，如果是，则退栈，继续找。否则，在栈顶的决策区间里二分查找，决策最优的最左位置是，把栈顶的决策结束位置设为，并把决策压入栈，决策起始位置为，结束位置为，需要注意的是当就无须入栈了。

给出代码：

#include <bits/stdc++.h>
#define int long long 

using namespace std;

const int N = 5e4 + 5;

int n, L, c[N], top, sum[N], f[N];

struct Htucp {
	int l, r, x;
	Htucp () {}
	Htucp (int _l, int _r, int _x) :
		l (_l), r (_r), x (_x) {}
} stk[N];

inline int w (int i, int j)
{
	int res = sum[j] - sum[i] - L;
	res += j - i - 1;
	return res * res;
}

inline int find (int i)
{
	int l = stk[top].l, r = stk[top].r, mid;
	while (l <= r)
	{
		mid = l + r >> 1;
		if (f[i] + w (i, mid) < f[stk[top].x] + w (stk[top].x, mid))
			r = mid - 1;
		else
			l = mid + 1;
	}
	return l;
}

signed main ()
{
	int cur = 1;
	scanf ("%lld %lld", &n, &L);
	for (int i = 1; i <= n; i ++)
	{
		scanf ("%lld", &c[i]);
		sum[i] = sum[i - 1] + c[i];
	}
	stk[top = 1] = Htucp (1, n, 0);
	for (int i = 1; i <= n; i ++)
	{
		f[i] = f[stk[cur].x] + w (stk[cur].x, i);
		while (i < stk[top].l && f[i] + w (i, stk[top].l) < f[stk[top].x] + w (stk[top].x, stk[top].l))
			top --;
		int u = find (i);
		stk[top].r = u - 1;
		if (u <= n)
			stk[++ top] = Htucp (u, n, i);
		if (i == stk[cur].r)
			cur ++;
	}
	printf ("%lld", f[n]);
	return 0;
}

当然我不会告诉你这题可以用斜率优化写。

时间复杂度是我们可以优化的，既然这么提到了，说明我们要开始优化了。

SMAWK

首次提出完全单调矩阵的线性求解行最小算法的是五位学者是、、、、（其实这里写的所有大写字母是一个记录机房座位同学的排列）。

但是只适用于离线情况，没有类似分治算法的移动指针性质，但只需要计算个元素的取值以得到每行的最小值。

Reduce

当求解最小值的矩阵的行数少而列数多的时，有很多列冗余，删除它们对答案没有影响，故考虑这个子过程—— 。

是一个的完全单调矩阵（子矩阵都是单调矩阵的矩阵），其返回一个的矩阵，结果为删除若干冗余的列得到的矩阵。

至于冗余位置，当一个位置不可能是当前行的最小值位置，那么称为冗余位置。

初始定义，当时结束过程，否则开始比较和。

若，删除第列，，回到比较步骤；

若，且，删除第列，回到比较步骤；

若且，向右移动指针，回到比较步骤。

可以看一下这张图

我们目前维护的矩阵显然在对角线以上（不包括对角线）的必定是冗余位置，否则中间一定有冗余列。

若，那么显然整个第列都是冗余列，因为部分已经确认为冗余位置，而也被确定为冗余位置也直接导致整列被确定为冗余列，直接删掉就好。

若且，那么下一列必然是冗余列，删除即可，否则还不能确定下一列是否为冗余列，往右移动指针。

给出这个过程的代码（使用链表，等等我好像不会链表）：

inline void del (int x)
{
	if (pre[x] != -1)
		suf[pre[x]] = suf[x];
	else
		P = suf[x];
	pre[suf[x]] = pre[x];
}
vector <int> Reduce (vector <int> X, vector <int> Y)
{
	for (int i = 0; i < Y.size (); i ++)
	{
		pre[i] = i - 1;
		suf[i] = i + 1;
	}
	int x = 0, y = 0;
	for (int i = Y.size () - X.size (); i > 0; i --)
	{
		if (mp[X[x]][Y[y]] > mp[X[x]][Y[suf[y]]])
		{
			y = suf[y];
			del (pre[y]);
			if (x)
			{
				y = pre[x];
				x --;
			} 
		}
		else
		{
			if (x == X.size () - 1)
				del (suf[y]);
			else
			{
				y = suf[y];
				x ++;
			}
		}
	}
	vector <int> ret;
	vector (int i = P; i != Y.size (); i = suf[i])
		ret.push_back (Y[i]);
	return ret;
}

这个过程会删除列，的最大值为，而每次比较会导致减一并删除列数加一，或者加一，所以复杂度为。

直接暴力实现矩阵的任意列删除复杂度是不能接受的，因此实现时可以用链表维护未被删除的列的编号，这样可以删除列。

主体

这是一个递归算法，借用作为子过程，过程表示计算的完全单调矩阵的每行最小值所在列。

若的时候直接计算答案，设，。递归计算得到偶数行最小值所在列。对于中的奇数行，在其相邻两行的最小值所在列之间暴力枚举计算出最小值所在列。

由于有了相邻两行的限制，最后一步复杂度。需要注意由于在递归过程中删除了若干中间的列，所以回溯的时候要注意列编号的维护。

void MSAWK (int vector <int> X, vector <int> Y)
{
	Y = reduce (X, Y);
	if (X.size () == 1)
	{
		M[X[0]] = Y[0];
		return ;
	}
	vector <int> Z;
	for (int i = 0; i < X.size (); i ++)
		if (i % 2 == 0)
			Z.push_back (X[i]);
	MSAWK (Z, Y);
	for (int i = 0; i < X.size (); i ++)
	{
		if (i % 2 == 0)
			continue;
		int l = lower_bound (Y.begin (), Y.end (), M[X[i - 1]]) - Y.begin ();
		int r = 0;
		if (i == X.size () - 1)
			r = Y.size () - 1;
		else
			r = lower_bound (Y.begin (), Y.end (), M[X[i + 1]]) - Y.begin ();
		M[X[i]] = Y[l];
		while (l < r)
		{
			l ++;
			if (mp[X[i]][Y[l]] < mp[X[i], M[X[i]]])
				M[X[i]] = Y[l];
		}
	}
}

矩阵优化

~~这是最简单的矩阵规划问题。~~

线性常系数递推方程

这里需要知道的是矩阵乘法，设为的矩阵，为的矩阵，设矩阵为矩阵和的乘积，其中矩阵中的第行第列元素可以表示为：

$C_{i,j}=\sum_{k=1}^MA_{i,k}B_{k,j}$

这里比较经典就是有关斐波那契数的题目，都很基础：

斐波那契数列

大家都知道，斐波那契数列是满足如下性质的一个数列：
$F_n=\left\lbrace \begin{aligned}{} 1\ \ (n\leq 2)\\\\ F_{n-1}+F_{n-2}\ \ (n\geq 3)\\\\ \end{aligned} \right.$
现在请求出的值。

~~很简单，递推，小朋友都会。~~

但是时间会如同不断膨胀的气球，最后，砰。所以考虑矩阵加速递推，也就是推出一个用于两个答案中间转移的矩阵。

要使，即。

因为，所以的第一列应该是。这样在进行矩阵乘法运算的时候才能令和相加，从而得到。同理，为了得到，矩阵的第二列应该为。

综上所述，。

给出核心的代码：

struct Matrix {
	int a[3][3];
	Matrix () { memset (a, 0, sizeof a); }
	Matrix operator * (const Matrix &b) const {
		Matrix res;
		for (int i = 1; i <= 2; i ++)
			for (int j = 1; j <= 2; j ++)
				for (int k = 1; k <= 2; k ++)
					res.a[i][j] = (res.a[i][j] + a[i][k] * b.a[k][j]) % mod;
		return res; 
	}
} ans, base;

碰到这类题目主要是推算一个稀里糊涂的矩阵。

一些题目

~~这是最简单的动态规划问题……不对这好像是一堆乱七八糟的问题。~~

切割

煌正在教伊芙利特数学，今天讲到关于切割多边形的问题，煌为了让她明白，于是举了一个例子。

伊芙利特有一块形为个顶点的正多边形的酒精巧克力，现在煌要用电锯帮她切成份，每一次可以沿着某个多边形的弦（顶点与顶点的连线）进行切割，将这个多边形一分为二。假设这个巧克力很奇怪，每个顶点都是不同的，那么对于一个正方形（个顶点的正多边形），煌有种方法切割它，沿着两条对角线切割或者根本不切割。但是如果要将其切割成份则只有种方法；要将其切成份是不可能的（注意每一次切割我们只对一个多边形操作，不能一次将个三角形切成个三角形）

因为切法数目可能很多，只要求算出切法总数模的余数，伊芙利特想不出这个问题，于是她把这个问题丢给了你，希望身为巴别塔的毁灭者的你可以解决这个问题，不然她会把你烧成黑炭。

既然我们讲的是动态规划，所以我们用的就是动态规划（像废话）。

因为题目里比较清楚的几个状态是多边形的边数，切割成的份数，所以我们借此设状态表示边形切成份的方案数。

比如现在有一个五边形，我们要将其分成三份，我们先给它标号：

蚀刻章

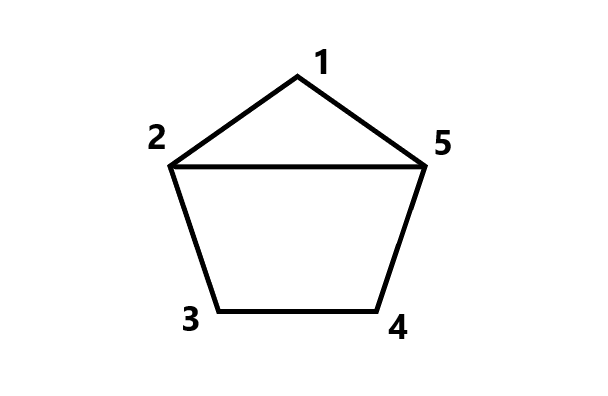
那么我们考虑号点时是否有切割，即是否有切线以号点为端点。如果方案中没有切线过号点，方案数就是，将其分为两种情况，一种是这样：

啊……好痛！

也就是将其分成一个三角形和一个四边形，这里的方程就是，因为我们已经分出了一个三角形，要将剩下的边形分成份。

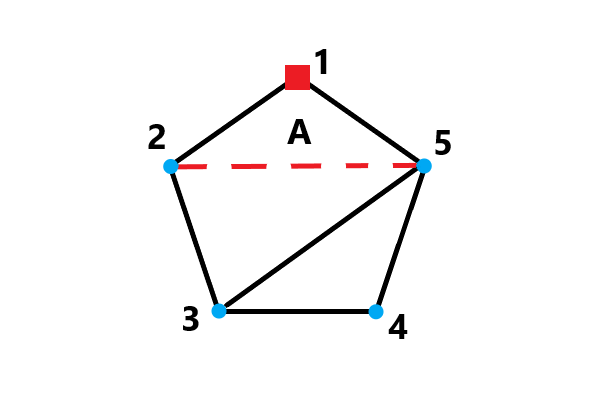
还有一种比较难理解：

超级难理解的

至于，即将上面那个点屏蔽掉（但是我们这边还是初始情况），能用的点只有除了号点以外的点，比如现在就是个点，那么在这个五边形中将其分成份。或者你也可以看做不拿上面的三角形却还要把这个五边形分成份，当然在这里是不可能的。

然后考虑有切线穿过了号点，那么我们枚举所有过点切线中的另一个端点的最小值是多少，假设是，那么我们将边形分成了的多边形和的多边形，因为我们枚举的是最小值，故的多边形的划分方案中就不存在切线过点的方案，否则与我们枚举的最小值矛盾。

然后我们枚举这份分别怎么分配给这两个多边形，假设分到了份，则分了份，因为是一个边形，是一个边形，故方案数为，用那个乘法原理，所以是相乘，至于前面那个东西应该很熟悉，如果不懂可以向上爬去找找。

核心代码给出：

if (k > n - 2)
	return printf ("0") & 1;
for (int i = 1; i <= n; i ++)
	f[i][1] = 1;
for (int i = 4; i <= n; i ++)
	for (int j = 2; j <= min (i - 2, k); j ++)
	{
		f[i][j] = (f[i - 1][j] + f[i - 1][j - 1]) % p;
		for (int u = 3; u <= i - 1; u ++)
		{
			int g = i - u + 2;
			for (int l = 1; l <= min (u - 2, j - 1); l ++)
				f[i][j] = (f[i][j] + (f[u - 1][l] + f[u - 1][l - 1]) * f[g][j - l] % p) % p;
		}
	}
printf ("%d", f[n][k]);

第一次用这个切割线，发现有许多特性，你甚至可以让这个剪刀和光标一起动，还可以让它很鬼畜地在原地抖抖抖抖抖抖抖抖抖抖。

大爹点兵

博卓卡斯替和霜星在巡视乌萨斯游击队。

爱国者将自己的每一个游击队步兵分为零一二级，共三种等级，爱国者想让游击队的步兵排成一长条，仅当一些情况下，他认为这样的队伍是整齐的：

1、这个队伍的所有前缀都是整齐的。

2、这个队伍中二级兵出现的个数不少于一级兵出现的个数。

3、这个队伍中一级兵出现的个数不少于零级兵出现的个数。

请你求出有多少个长度为的队伍是整齐的，由于答案很大，你只需要给出答案模的答案即可，如果你求不出答案，霜星就会把你冻成冰棍送给小火龙当儿童节礼物（更新的这个时候是儿童节呢，而且夏天很适合吃冰棒吧（笑））。

一眼就是构造题（好像也不算但是真的好像啊所以就当它是构造题吧），总之就是给一些可行排列然后算方案数的。

模拟赛的时候我还自信地在头文件下写了一行注释：

/ 显然数位，用普通不是直接飞 /

好，事实证明，使用普通的时间复杂度是的，对于前面的排列只需要枚举两个兵种的个数就彳亍了，另一个可以靠当前兵数减出来。

所以我们的状态就设出来了，一个是当前兵数，一个是当前放的二级兵数，还有一个是当前放的一级兵数。

关键是空间复杂度，出题人比较毒瘤，开了，然后结果还是的，这是人干的事吗……

但是其实发现，第一可以使用滚动数组；第二，每个兵种不都一定是个，零级兵最多放个，一级兵最多放个，二级兵最多放个。

所以最后经过深思熟虑后的状态是，当前的一级兵个数，表示当前的零级兵个数。

这个，很巧妙的压掉了一维但其实没有完全压掉（我在说什么），注意这里不能逆推，因为是一个一个放的，不能像背包问题一样，所以我们把当前放的个数压成奇数形态，或者偶数形态，这个东西就是用处不大也对答案没什么贡献但是不加又过不了的那种东西。

考虑四种情况。

第一种情况，当一级兵的个数比二级兵的个数多（至于为什么这边不考虑零级兵是因为零级兵的循环范围比一级兵还小），这个时候直接跳过。

第二种情况，二级兵的个数比一级兵的个数多，我们上面也说了所以可以不用考虑零级兵，放一级兵或者零级兵：

$f[j][k][1/0]=f[j-1][k][1/0]+f[j][k-1][1/0]+f[j][k][1/0]$

第三种情况，当前一级兵比零级兵多，放零级兵：

$f[j][k][1/0]=f[j][k-1][1/0]+f[j][k][1/0]$

第四种情况，这个时候就是放二级兵了：

$f[j][k][1/0]=f[j][k][1/0]$

最后一个竟和没写没啥区别。

目前可公开的核心代码（突然想起这个梗了，之前周六留下来准备去吃晚饭的时候听到了，现在想起来了）：

for (int i = 1; i <= n; i ++) // 枚举第几个兵  
	for (int j = 0; j <= i; j ++) // 枚举一级兵  
		for (int k = 0; k <= j; k ++) // 枚举零级兵  
		{
			if (j >= i - j - k) // 第一种情况 
				break;
			else if (j <= i - j - k) // 第二种情况  
				f[j][k][i & 1] = ((j ? f[j - 1][k][(i - 1) & 1] : 0) + (k ? f[j][k - 1][(i - 1) & 1] : 0) + f[j][k][(i - 1) & 1]) % mod;
				// 这里注意判一下 j 和 k 的出界情况，弄成负数就不好了  
				else if (k <= j - 1) // 第三种情况 
					f[j][k][i & 1] = ((k ? f[j][k - 1][(i - 1) & 1] : 0) + f[j][k][(i - 1) & 1]) % mod;
					else if (i - j - k > 0)
						f[j][k][i & 1] = f[j][k][(i - 1) & 1] % mod;
		}
for (int i = 0; i <= n; i ++) // 枚举一级兵  
	for (int j = 0; j <= i; j ++) // 枚举零级兵  
		if (i <= n - i - j && j <= i) // 这个方案属实可以  
			ans = (ans + f[i][j][n & 1]) % mod;

我还是用这个切割线吧，好像不能手造切割线……然后接下来给大家看一道和上面这道很像但不是构造题的题。

源石装箱员

兔子谷矿区是泰拉大陆一个不秘密开采源石的地方，由于开采源石的难度非常高，所以开采出的会有三种纯度不同的源石矿物，分别是，和的源石矿物（这落差也是没谁了）。为了出售方便，必须把不同纯度的源石分开装箱，装箱员暴行第一次从流水线上取十个源石（如果一共不足十个，则全部取出），以后每一次把手中某种纯度的源石放进相应的箱子，然后再从流水线上顺序取一些源石，使手中保持十个源石（如果把剩下的取出不足十个，则全部取出），如果所有的源石都装进了箱子，那么暴行的任务就完成了。

由于装箱是很累的事情，所以暴行希望能以最少的装箱次数来完成她的任务，如果你不告诉她这个答案，她就会把拖把抡你脸上。

啊……这个题的状态，因为我说和前面那题是差不多的所以大家知道了吧……而且这题的范围特小，只有，甚至允许我们飞。

对于这题，决策就是要不要把手里源石丢到箱子里去，所以状态很简单，用来表示拿到第个源石，手里拿了颗的源石，颗的源石，颗的源石，最后答案是。

对于丢源石，因为是将同一种丢完，所以一维状态在那个时候甚至会归零：

$f[i][0][k][l]=\min(f[i][0][k][l],f[i][j][k][l]+1);$

然后记得特判一下三种源石数量超过十个的情况，代码直接给出：

for (int i = 1; i <= n; i ++)
{
	for (int j = 0; j <= 10; j ++)
	{
		for (int k = 0; k <= 10; k ++)
		{
			for (int l = 0; l <= 10; l ++)
			{
				if (j + k + l > 10)
					continue;
				if (a[i] == 'A' && j)
					f[i][j][k][l] = f[i - 1][j - 1][k][l];
				if (a[i] == 'B' && k)
					f[i][j][k][l] = f[i - 1][j][k - 1][l];
				if (a[i] == 'C' && l)
					f[i][j][k][l] = f[i - 1][j][k][l - 1];
				f[i][0][k][l] = min (f[i][0][k][l], f[i][j][k][l]);
				f[i][j][0][l] = min (f[i][j][0][l], f[i][j][k][l]);
				f[i][j][k][0] = min (f[i][j][k][0], f[i][j][k][l]);
			}
		}
	}
}
printf ("%d", f[n][0][0][0]);

接下来来讲一道转移上很妙的题目，看懂了会非常简单（真的）。

盟友下棋

今天晚上，银灰和博士在宿舍里下中国象棋。

在行列的棋盘上，银灰想放若干个炮（当然可以一个都不放），使得每一个炮不能攻击到另一个炮，问有多少种放置方法。

不会有人不知道炮的攻击方法吧……不知道百度，因为答案可能很大，所以只需要输出答案模。

如果你不告诉他答案，他就不会当你的盟友。

棋盘大小是，所以暴力可以获得分的好成绩。

然后这个数据我们选择，如果不是我在做这题之前说“这数据不是显然爆搜”。

考虑到合法状态，每一行和每一列炮的数量必定小于三，所以用数组记有几列放了一个炮，有几列放了两个炮，这样记是因为不用记录棋盘的完整状态，那个没用。

设状态为转移到行，有列放了一个棋子，有列放了两个棋子，那么放了零个棋子的有列。

然后分类讨论就可以了。

不放棋子，直接继承前一行的状态：

$f[i][j][k]=f[i-1][j][k]$

1	f[i][j][k] = f[i - 1][j][k];

这一行只放一个棋子，然后我们肯定不会在已经有两个棋子的那些列放，因此存在两种情况。

放在有一个棋子的列：

$f[i][j][k]+=f[i-1][j+1][k-1]\times(j+1)$

因为这原来一个棋子的这一列变成了两个棋子的，所以表示一个棋子列少一个，表示两个棋子的多一个，然后原来有个一个棋子的列，就反正这些列都可以放。

1 2	if (k >= 1) f[i][j][k] += f[i - 1][j + 1][k - 1] * (j + 1);

放在没有棋子的列：

$f[i][j][k]+=f[i-1][j-1][k]\times(m-(j-1)-k)$

因为原来没有棋子的列变成了有一颗棋子的列，所以，然后原来有个只有一颗棋子的列，所以这里没有棋子的有列。

1 2	if (j >= 1) f[i][j][k] += f[i - 1][j - 1][k] * (m - j - k + 1);

这一行放两颗棋子，然后我们和上面一样，不会把棋子放在已有两个棋子的列，因此存在三种情况：

一个放在有一颗棋子的列，另一个放在没有棋子的列：

$f[i][j][k]=f[i-1][j][k-1]\times j\times(m-j-(k-1))$

那么有原来有一颗棋子的那列变成两颗棋子，原来没有棋子的列变成一颗棋子，现在一颗棋子的列不增不减，反而是两个棋子的那一列，所以，然后根据乘法原理，后面的选择乘起来。

1 2	if (k >= 1) f[i][j][k] += f[i - 1][j][k - 1] * j * (m - j - k + 1);

都放在没有棋子的列：

$f[i][j][k]=f[i-1][j-2][k]\times C_{m-(j-2)-k}^2$

显然一个棋子的列加两个，然后这两个棋子选择放在原本没有棋子的列中，那一共是列，用组合数公式。

1 2	if (j >= 2) f[i][j][k] += f[i - 1][j - 2][k] * C (m - j - k + 2);

都放在有一个棋子的列：

$f[i][j][k]=f[i-1][j+2][k-2]\times C_{j+2}^2$

原本一个棋子的列少两个，两个棋子的列现在加两个，然后在一个棋子的列共列中选出两列放。

1 2	if (k >= 2) f[i][j][k] += f[i - 1][j + 2][k - 2] * ((j + 2) * (j + 1) / 2);

完整代码：

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int mod = 9999973;
const int N = 101;

int n, m, ans;
int f[N][N][N];

inline int C (int x)
{
	return (x * (x - 1) / 2) % mod;
}

signed main ()
{
	scanf ("%lld %lld", &n, &m);
	f[0][0][0] = 1;
	for (int i = 1; i <= n; i ++)
	{
		for (int j = 0; j <= m; j ++)
		{
			for (int k = 0; k <= m - j; k ++)
			{
				f[i][j][k] = f[i - 1][j][k];
				if (k >= 1)
					f[i][j][k] += f[i - 1][j + 1][k - 1] * (j + 1);
				if (j >= 1)
					f[i][j][k] += f[i - 1][j - 1][k] * (m - j - k + 1);
				if (k >= 2)
					f[i][j][k] += f[i - 1][j + 2][k - 2] * ((j + 2) * (j + 1) / 2);
				if (k >= 1)
					f[i][j][k] += f[i - 1][j][k - 1] * j * (m - j - k + 1);
				if (j >= 2)
					f[i][j][k] += f[i - 1][j - 2][k] * C (m - j - k + 2);
				f[i][j][k] %= mod;
			}
		}
	}
	for (int i = 0; i <= m; i ++)
		for (int j = 0; j <= m; j ++)
			ans = (ans + f[n][i][j]) % mod;
	printf ("%lld", (ans % mod + mod) % mod);
	return 0; 
}

啊又是一道非常有意思的题目。

消失的小饼干

真理刚烤完了块彼得海姆畅销饼干，它们面积分别是，由于她的疏忽，第块丢失了。

要用剩下的块饼干装满面积为的盘子，有几种方法呢。

显然有很多方法，但是真理只需要你告诉她模的答案即可，如果你不告诉真理，凛冬就会让你去见历史上伟大的马克思主义者。

*本品牌仅服务于泰拉地区，与现实生活中的权威公司无关。

嗯……是一道看得出的背包问题，它出现在了模拟赛里。

但是！我看过了！所以我看到时候的时候先是惊喜了一下。

然后就悲伤了，因为我当时没有做，所以现在记录下来。

总之就是去掉一个东西然后再让你跑背包，那么要来了！暴力！

嗯…… 果断时间爆炸！所以这里要用到一下下容斥，比较可以想到的就是可行方案就是所有方案减去不用这家伙的方案。

少了某件物品也就是少了一次这样的转移，直接来看代码啦：

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int mod = 1e9 + 7;
const int N = 1e4 + 1; 

int n, m;
int w[N], f[N], g[N];

signed main ()
{
	scanf ("%lld %lld", &n, &m);
	for (int i = 1; i <= n; i ++)
		scanf ("%lld", &w[i]);
	f[0] = 1;
	for (int i = 1; i <= n; i ++)
		for (int j = m; j >= w[i]; j --)
			f[j] = (f[j] + f[j - w[i]]) % mod; // 计算那个总方案！
	for (int i = 1; i <= n; i ++)
	{
		memset (g, 0, sizeof (g));
		g[0] = 1;
		for (int j = 1; j <= m; j ++)
		{
			if (w[i] > j)
				g[j] = f[j] % mod; // 这个就是常规操作，背包空间不够嘛
			else
				g[j] = (f[j] - g[j - w[i]] + mod) % mod;
		}
		printf ("%lld\n", g[m]);
	}
	return 0;
}

当然也可以先跑一遍然后再跑一遍，等于是还原操作：

for (int i = 1; i <= n; i ++)
{
	for (int j = w[i]; j <= m; j ++)
		f[j] = (f[j] - f[j - w[i]] + mod) % mod;
	printf ("%lld\n", f[m]);
	for (int j = m; j >= v[i]; j --)
		f[j] = (f[j] + f[j - w[i]]) % mod;
}

来给出一道以前模拟赛的题，但是当时因为水平太烂没有做出来。

三……嘭！

现在需要做个炸药，但是做炸药的成本是很高的，所以会用到源石技艺，现有两种操作：

1、用源石技艺做出一个炸药或者销毁一个炸药，代价为。

2、用精妙的源石技艺将已经做出来的炸药复制一份，代价为。

值得一提的是，开始没有炸药。

现在她想让你告诉她做个炸药的最小代价，不然她会把这一批大当量炸药全部放在你的卧室里。

其实这次做到了也没有做出来，果然还是太烂了。

但是其实是一个简单推方程的题目，首先设计状态为让个炸药变到个炸药的代价。

然后你就去考虑分类讨论。

如果当前是偶数的话，肯定只能从和转移过来的。

如果在使用减操作，由转移过来，那么从转移过来，因为是个奇数，第一只能从偶数转移过来，第二你总不可能再从使用加操作转移过来吧……然后由转移过来，那么这中间就产生了……我看看啊…… 的代价。

但是如果直接从转到再转到，这只需要的代价，上面那个简直是亏到家了。

所以当为偶数时，不会从转移过来。你可能会问我为什么不能从转移到，主要还是因为我们讨论的是转移到的最佳策略，和是没有什么关系滴！

所以这个方程是：

$f_i=\min(f_{i-1}+x,f_{\frac{i}{2}}+y)$

如果当前是奇数的话，可以从和转移过来。

但是还未确定，而且前面也说过，它不会从转移过来，根据前面的结论，只能从转移过来，所以：

$f_i=\min(f_{i-1}+x,f_{\frac{i+1}{2}}+x+y)$

基本代码如下：

f[1] = x;
for (int i = 2; i <= n; i ++)
{
	f[i] = f[i - 1] + x;
	if (i & 1)
		f[i] = min (f[i], f[(i + 1) / 2] + x + y);
	else
		f[i] = min (f[i], f[i / 2] + y);
}

然后来讲一道必讲的题目，呃好吧其实我也不是觉得必讲，但是真的很有意思……

宿舍今天的健康餐

芙蓉是一个擅长做菜的医疗干员，她共掌握种烹饪方法，且会使用种主要食材做菜。为了方便叙述，我们对烹饪方法从编号，对主要食材从编号。

芙蓉做的每一道菜都将使用恰好一种烹饪方法与恰好一种主要食材。更具体地，芙蓉会做道不同的使用烹饪方法和主要食材的菜，这也意味着芙蓉总共会做道不同的菜。

芙蓉今天要准备一桌菜招待博士和炎熔，然而三个人对菜的搭配有不同的要求，更具体的，对于一种包含道菜的搭配方案而言：

1、芙蓉不会让大家饿肚子，所以将做至少一道菜，即。

2、炎熔希望品尝不同烹饪方法做出的菜，因此她要求每道菜的烹饪方法互不相同。

3、博士不希望品尝太多同一食材做出来的菜，因此他要求每种主要食材至多在一半的菜（即道菜）中被使用。

这些要求难不倒芙蓉，但她想知道共有多少种不同的符合要求的搭配方案。两种方案不同，当且仅当存在至少一道菜在一种方案中出现，而不在另一种方案中出现。

身为博士的你只需要告诉芙蓉所有要求的搭配方案数对取模的结果即可，如果你没有给出答案，你会天天吃芙蓉做的健康餐。

题意就是给一个矩阵然后求合法方案数，然后这个合法方案要注意的就是某一列里的主要食材是不能超过总共选的一半的（每一行表示了主要食材，每一列表示了烹饪方式），而且只会有一列不合法，因为不可能有两列都超过选的一半，如果还没有听懂可以考虑类似这样的一个表格：

比如这就是一种不合法的方案

也就是说烹饪方法只能使用一种，但是一道菜可以用多个主要食材，做多少道这样的菜也不同。

那么看到这种算方案数的题目，我们优先想想枚举这个方案麻烦不麻烦，如果麻烦就尝试使用容斥吧。

对于这个题目，我们可以使用容斥，也就是每行选不超过一个的方案数减去每行选不超过一个，且某一列选了超过一半的方案数，然后我们来枚举那一个不合法的列。

接下来来设计状态，用表示对于这一列，前行在这一列中选了个，其他列选了个，那么令为第行的总和，则有转移方程：

$f_{i,j,k}=f_{i-1,j,k}+a_{i,col}\times f_{i-1,j-1,k}+(s_i-a_{i,col})\times f_{i-1,j,k-1}$

如果看不懂我们可以慢慢拆这个式子，首先可以将其分为三个部分：

$f_{i-1,j,k}$

这个是前面的状态，这个应该不用多说。

$a_{i,col}\times f_{i-1,j-1,k}$

对于选第行，从前面这一行，即还没有选择第行的状态，那此时获得加一，因为这一列得到的食材加一，然后获得加一，总体加一。

$(s_i-a_{i,col})\times f_{i-1,j,k-1}$

对于这一行不给这一列的情况，对于这一行的和减去这一格，因为不用在意给其他什么列，反正就不是给它的，这个是没有关系的，然后至于转移和上面是一样的，其他列获得加一。

时间复杂度是，因为太差了所以我们要开始优化了。

然后发现其实我们不用考虑其他行的个数，也就是我们前面考虑的，其实只用看相对大小即可，所以我们可以压掉最后这一维，我们把状态表示为，表示前行，当前列的数比其他列多了个，则有新转移方程了：

$f_{i,j}=f_{i-1,j}+a_{i,col}\times f_{i-1,j-1}+(s_i-a_{i,col})\times f_{i-1,j+1}$

这里感觉转移的话（如果前面你好好看了），是非常好懂的！！！

这边就是拉开了差距，就是减小了差距。

总方案数就是再开一个用的数组，再设计一个大家肯定都知道的状态为前行共选了个数，然后转移方程如下：

$g_{i,j}=g_{i-1,j}+s_i*g_{i-1,j-1}$

总复杂度就会降为，代码如下：

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int mod = 998244353;

const int N = 101;
const int M = 2e3 + 1;

int n, m, a[N][M], sum[N][M], g[N][N], f[N][N * 2], ans;

signed main ()
{
	scanf ("%lld %lld", &n, &m);
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= m; j ++)
		{
			scanf ("%lld", &a[i][j]);
			sum[i][0] = (sum[i][0] + a[i][j]) % mod;
		}
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= m; j ++)
			sum[i][j] = (sum[i][0] - a[i][j] + mod) % mod;
	for (int col = 1; col <= m; col ++)
	{
		memset (f, 0, sizeof f);
		f[0][n] = 1;
		for (int i = 1; i <= n; i ++)
			for (int j = n - i; j <= n + i; j ++)
				f[i][j] = (f[i - 1][j] + f[i - 1][j - 1] * a[i][col] % mod + f[i - 1][j + 1] * sum[i][col] % mod) % mod;
		for (int i = 1; i <= n; i ++)
			ans = (ans + f[n][n + i]) % mod;
	}
	g[0][0] = 1;
	for (int i = 1; i <= n; i ++)
		for (int j = 0; j <= n; j ++)
			g[i][j] = (g[i - 1][j] + (j > 0 ? g[i - 1][j - 1] * sum[i][0] % mod : 0)) % mod;
	for (int i = 1; i <= n; i ++)
		ans = (ans - g[n][i] + mod) % mod;
	printf ("%lld", ans * (mod - 1) % mod); // 这里是取反，具体看下面解释  
	return 0;
}

看一下最后的取反：

$(ans\times mod-ans)\%mod=-ans\%mod$

至于为什么要取反，是因为我们做的是非法方案减去全部方案，所以取个反就行了。

接下来记录一道经典的题目。

花盆

波登可有两列花盆，她想让这两列花变得一模一样，现在她决定做三种操作：

1、移除一盆花

2、放入一盆花

3、将一盆花改为另一盆花

她不想太累，所以她想知道将第一列花改成第二列花的最小操作次数，希望你能告诉她，不然她会对你使用花香疗法。

非常经典的序列题，在这里设的状态也比较难想，表示第一列有盆花，第二列有盆花时最少需要几次才能改成相同。

递推过去，如果第个相同就不用改，方程即：

$f[i][j] = f[i-1][j-1]$

不然就考虑三种情况。

第一种，如果能将转换为，那就可以将删掉：

$f[i][j]=f[i-1][j]+1$

第二种，如果能将转换为，那就可以把删掉：

$f[i][j]=f[i][j-1]+1$

第三种，如果能将转换为，那就可以把变为：

$f[i][j]=f[i-1][j-1]+1$

然后在其中取最小值，主要代码如下：

for (int i = 1; i <= n; i ++)
	f[i][0] = i;
for (int i = 1; i <= m; i ++)
	f[0][i] = i;
for (int i = 1; i <= n; i ++)
	for (int j = 1; j <= m; j ++)
	{
		if (a[i] == b[i]) // 两盆花相同  
			f[i][j] = f[i - 1][j - 1]; // 所以直接转移  
		else
			f[i][j] = min (f[i - 1][j], min (f[i][j - 1], f[i - 1][j - 1])) + 1; // 挑选一种情况  
	}

接下来是一道使用拓扑排序的题，因为碰到了所以就随手记录一下吧（虽然说难度并不是很大）。

信仰号街车

愿光芒铺陈你的前路，愿虔诚与信念永伴你身。

空弦正在麦田中闲逛，在这片巨大的麦田里，有许多修道院，麦田中有一些单向路能够连接修道院，而且保证这些路没有环。

现在空弦希望从号修道院走到号修道院，问在距离不超过情况下空弦最多经过多少个修道院，并输出这个方案。

如果你不告诉她答案的话，她会在舰桥上让你当她的靶子。

因为是有向无环图，所以我们可以考虑使用拓扑排序。

然后我们考虑设计状态，这个地方我们定义为从出发到点走个点的最短路径。

因为拓扑的一个重要性质就是只有入度为的点才能处理，满足无后效性。

于是可以参考最短路的转移来设计方程：

$f_{u,i}=\min\lbrace f_{u,i},f_{u,i-1}+dis_{u,j}\rbrace$

输出路径的时候就在当时记录下来然后用栈全部一坨输出出来，完整代码如下：

#include <bits/stdc++.h>

using namespace std;

const int N = 5e3 + 1;

int n, m, k;

struct Edge {
	int nxt, to, dis;
} edge[N << 1];

int head[N], cnt;

int in[N], f[N][N], pre[N][N], ans;

vector <int> s;
stack <int> path;

inline void add_edge (int u, int v, int w)
{
	edge[++ cnt] = (Edge) {head[u], v, w};
	head[u] = cnt;
}

queue <int> Q;

void toposort () // 拓扑
{
	for (int i = 1; i <= n; i ++)
		if (!in[i])
			Q.push (i);
	while (!Q.empty ())
	{
		int u = Q.front ();
		Q.pop ();
		s.push_back (u); // 记录应该走的路径
		for (int i = head[u]; i; i = edge[i].nxt)
			if ((-- in[edge[i].to]) == 0)
				Q.push (edge[i].to); 
	}
}

int main ()
{
	memset (f, 0x3f, sizeof (f));
	memset (pre, -1, sizeof (pre));
	scanf ("%d %d %d", &n, &m, &k);
	for (int i = 1, u, v, w; i <= m; i ++)
	{
		scanf ("%d %d %d", &u, &v, &w);
		add_edge (u, v, w);
		in[v] ++;
	}
	toposort ();
	f[1][1] = 0; // 从 1 开始且经过一个点的路径长为 0 
	for (int k = 0; k < s.size (); k ++)
	{
		int u = s[k]; // 枚举当前应该走的点 
		for (int i = head[u]; i; i = edge[i].nxt)
			for (int j = 2; j <= n; j ++)
				if (f[u][j - 1] + edge[i].dis < f[edge[i].to][j])
				{
					f[edge[i].to][j] = f[u][j - 1] + edge[i].dis; // 转移 
					pre[edge[i].to][j] = u; // 记录前驱 
				}
	}
	for (int i = n; i >= 1; i --)
		if (f[n][i] <= k) // 取最优解 
		{
			ans = i;
			break;
		}
	printf ("%d\n", ans);
	int pos = n, dep = ans;
	while (pos != -1) // 采集路径 
	{
		path.push (pos);
		pos = pre[pos][dep];
		dep --;
	}
	while (!path.empty ()) // 输出路径
	{
		printf ("%d ", path.top ());
		path.pop ();
	}
	return 0;
}