青春最小少年不会梦到生成树学姐

一边思考“今天的我哪怕能比昨天更善良一点就好了”一边去生活。——《青春猪头少年不会梦到兔女郎学姐》

最小生成树

最小生成树（MST），是一副联通加权无向图中一棵权值最小的生成树，所以其实是最小权重生成树的简称。

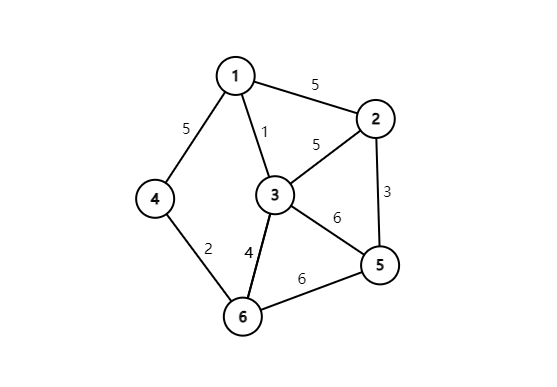
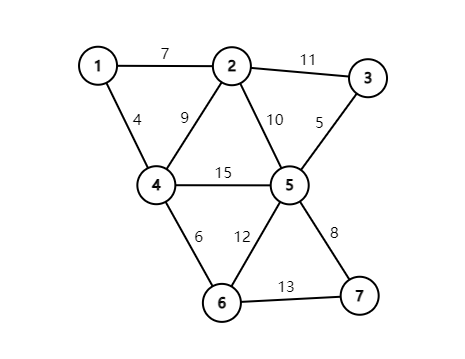
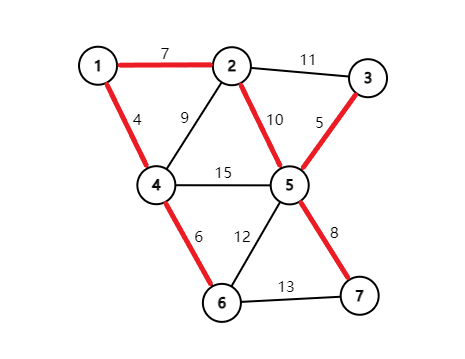
现在给出一个连通图 来说明一下这个贪得不行的最小生成树是什么：

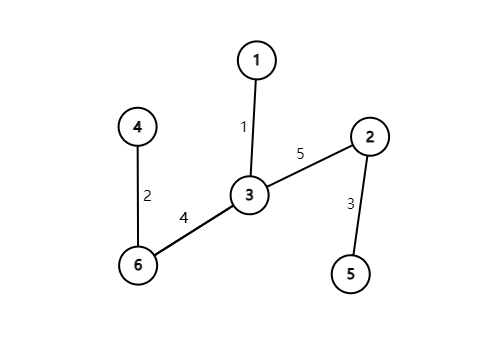
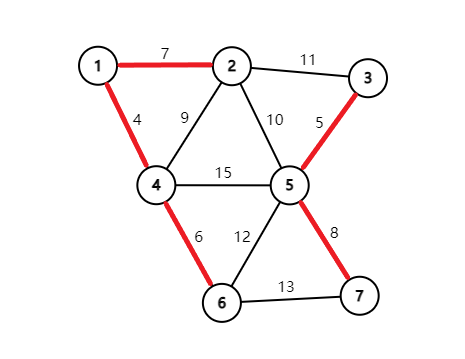
现在甲方于要求花最小代价把这个图连起来，所以我们这么连：

所以在给定的一个无向图 中，若 表示一条边的边权，若存在 为 的子集且为无循环图（本来都能联通的，多搞个三角形干啥对吧），使得 ，则此 为 的最小生成树。

有以下很明显的方程：

$$w(t)=\sum_{(u,v)\in t}w(u,v)$$

Kruskal

算法又叫加边法，因为我们会尝试把当前还未使用的边一条一条加进图中使得其联通。

预处理

为了贪，所以我们要把所有边按边权从小到大排序，这样就可以保证边权和最小，加边！加边！加边！对于两个已经连通的点，之后再碰到可以连通它们的边，这条边我不加，所以我们用一个并查集来维护每个点之间的连通关系（不会的话可以偷偷溜去《落第骑士并查集》）。

void init ()
{
	for (int i = 1; i <= n; i ++)
		fa[i] = i;
}
inline bool cmp (Edge x, Edge y)
{
	return x.w < y.w;
}

加边！

对于加边，我们在发现当前的边连通的两个点已经被连通了（并查集会记录），就不选择连，直到边数到达 就结束，对于 个点来说，连通它们， 条边是必须的。

来进行模拟（如果可以理解就直接跳过吧，因为这个我觉得真的很好理解的）：

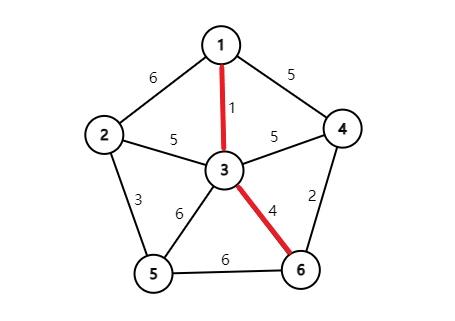
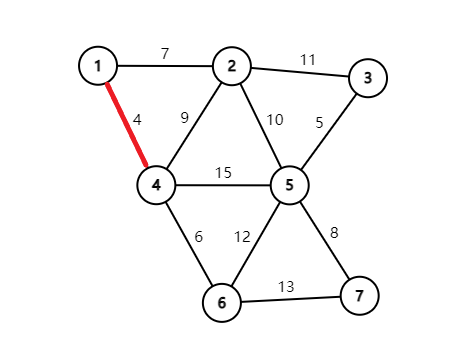
那么现在边权的排序是这样的：

$$cost=\lbrace1,2,3,4,5,5,5,6,6\rbrace$$

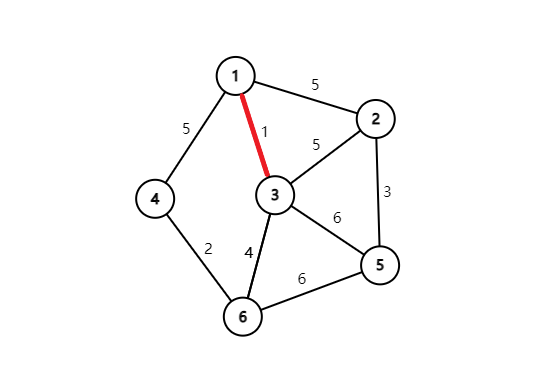
然后选择连上 号点和 号点：

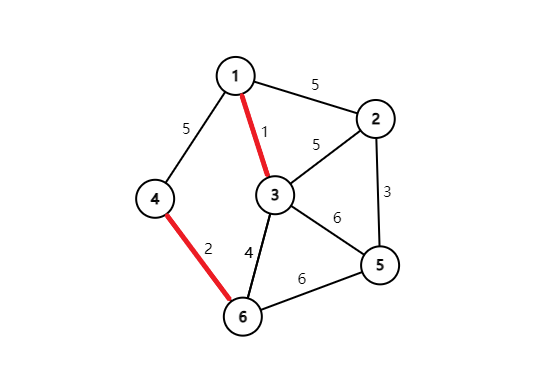
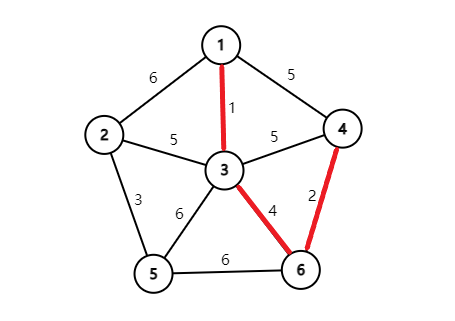
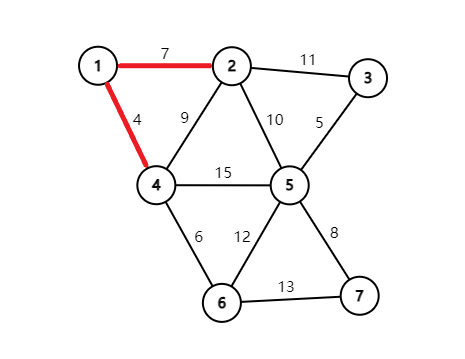
再连上 号点和 号点：

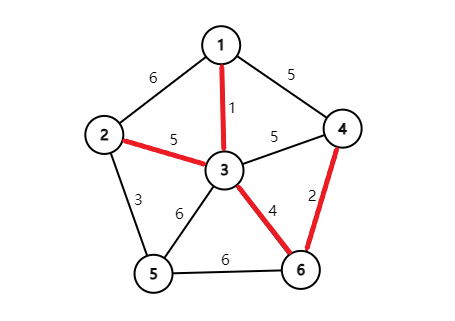
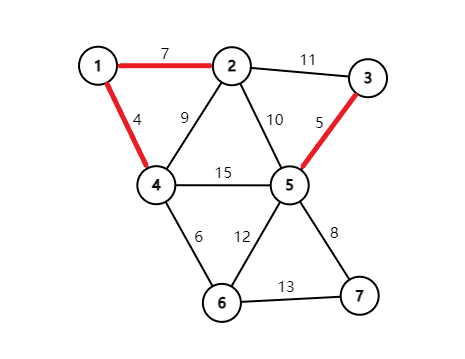
再连上 号点和 号点：

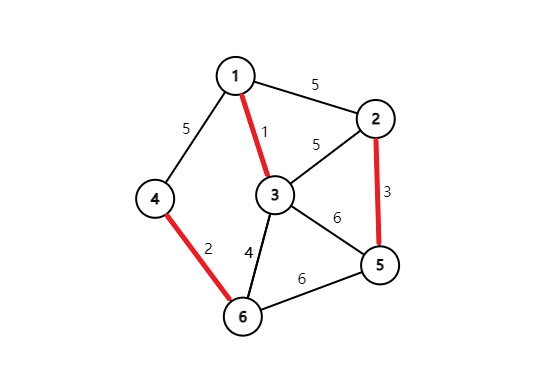
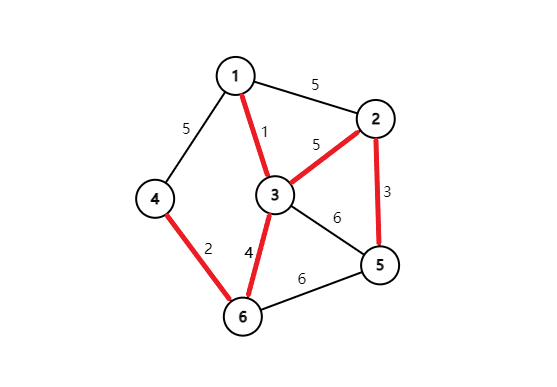
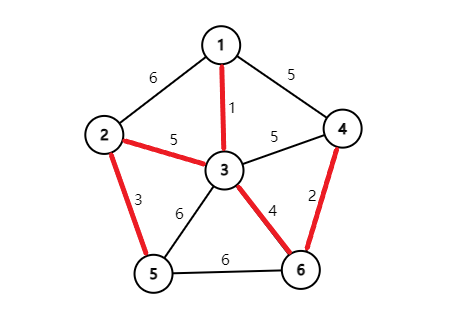
最终就会得到这么一张图：

给出主要代码：

void kruskal () // 最小生成树  
{
	sort (edge + 1, edge + m + 1, cmp);
	for (int i = 1; i <= m; i ++) // 这里还是要遍历 m 条边，因为前 n - 1 条边中可能有些边不会被连上
	{
		fx = find (edge[i].from), fy = find (edge[i].to); // 找本次要连的边两端的点各自的父节点
		if (fx == fy) // 如果它们已经连通
			continue;
		ans += edge[i].w; // 如果还未相连，就加入此边权 
		fa[fx] = fy; // 随便合并吧，想怎么合并怎么合并，按秩合并也可以 
		if (++ cnt == n - 1) // 现在这条边连上以后是否符合 n - 1 条边的条件
			break; // 直接结束吧，没必要浪费时间了（好像也不可以） 
	} 
}

时间复杂度是 。

Prim

预处理

有些大佬说 很像 ，好像确实，所以开始我们只需要把最短距离 预处理为 就彳亍了。

for (int i = 2; i <= n; i ++)
	dis[i] = inf; // 开始将最短距离全部定义为 inf

加点！

这回咱可就不一样了，这回我们咱们从点开始。

一般来说从 号点开始，对于当前点，每一次找一条它的最小扩展边。

初始时我们拥有两个集合，一个是已经被加入图的点集合，另一个是没有被加入的（好像是废话但是没有关系）。

$$in=\lbrace1\rbrace$$ $$out=\lbrace2,3,4,5,6\rbrace$$

然后现在的最小边权集合是这样的：

$$lowcost=\lbrace \infty,6,1,5,\infty,\infty\rbrace$$

然后其中最小边权是 的 ，所以选择顶点 ，更新已加入图的点集合：

$$in=\lbrace1,3\rbrace$$ $$out=\lbrace2,4,5,6\rbrace$$

因为加入了新的点，最小边权集合变成这样：

$$lowcost=\lbrace\infty,5,\infty,5,6,4\rbrace$$

现在最小边权是 ，所以选择顶点 ，更新集合：

$$in=\lbrace1,3,6\rbrace$$ $$out=\lbrace2,4,5,6\rbrace$$

因为加入了新的点，最小点边权集合变成这样：

$$lowcost=\lbrace\infty,5,\infty,\infty,2,6,\infty\rbrace$$

现在最小边权是 ，那么就连向 号点，我们的集合迎来了新的成员：

$$in=\lbrace1,3,6,4\rbrace$$ $$out=\lbrace2,5,6\rbrace$$

现在视角给到选手 号点，让我们来看看它的操作，显然它使得最小点权集合变成了这样：

$$lowcost=\lbrace\infty,5,\infty,\infty,\infty,6,\infty\rbrace$$

这样的扩展实则让到达 和 号点的最短距离没有更短，没有办法，接下来来连接第 个点。

然后现在的最小边权集合就是（大概其实我不给出心里都有数了）：

$$lowcost=\lbrace\infty,\infty,\infty,\infty,\infty,3,\infty\rbrace$$

最后一次会被更新成 ，最终得到这样的一棵最小生成树：

这里直接给出代码：

int prim ()
{
	for (int i = 2; i <= n; i ++)
		dis[i] = inf; // 开始将最短距离全部定义为 inf 
	for (int i = head[1]; i; i = edgr[i].nxt) // 对第一个点（起始点）进行遍历  
		dis[edge[i].to] = min (dis[edge[i].to], edge[i].w);
	while (++ tot < n) // 最小生成树的边数为 n - 1 
	{
		int minn = inf; // 接下来找最小边权  
		p = 1;
		vis[p] = 1; // 定义开始点已被访问过  
		for (int i = 1; i <= n; i ++) // 注意这里是对 n 个点进行遍历，不是连边，因为之后已被加入图的所有点都可向外扩展 
		{
			if (!vis[i] && minn > dis[i]) // 如果这个点未被访问且当前最短距离可行  
			{
				minn = dis[i]; // 记录下最小边权  
				p = i; // 记录下编号  
			}
		}
		ans += minn; // 统计一遍答案  
		for (int i = head[p]; i; i = edge[i].nxt) // 对当前编号的点前向星遍历  
		{
			int v = edge[i].to;
			if (dis[v] > edge[i].w && !vis[v])
				dis[v] = edge[i].w; // 更新 dis 数组 
		}
	}
	return ans;
}

可以用优先队列优化到 。

Borůvka

这是最早的最小生成树算法，是由 在 年发明的。

其实 就是一个多路增广的 ，每一次增广，会对现在的每一个连通块都找一遍最短边，最后每个连通块择优，将这些边全部连上。

预处理

其实它也使用了并查集来维护：

void init ()
{
	for (int i = 1; i <= n; i ++)
		fa[i] = i; // 刚开始每一个点都是一个连通块 
}

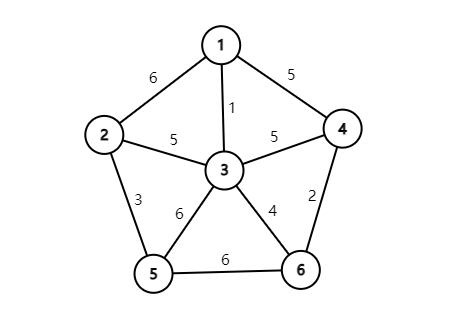
加连通块！

假设现在有这样一张图：

所以刚开始的连通块集合是这样的：

$$\lbrace1\rbrace\lbrace2\rbrace\lbrace3\rbrace\lbrace4\rbrace\lbrace5\rbrace\lbrace6\rbrace\lbrace7\rbrace$$

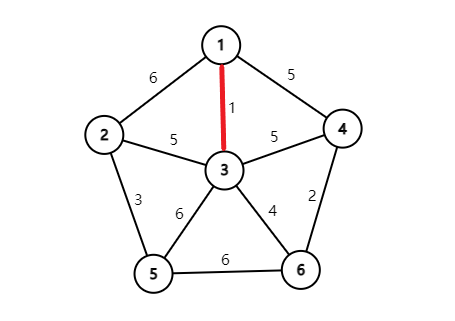
然后现在对每个点找一遍与它相连的最小权边，对 号点而言，是 ：

现在的连通块集合是这样的：

$$\lbrace1,4\rbrace\lbrace2\rbrace\lbrace3\rbrace\lbrace5\rbrace\lbrace6\rbrace\lbrace7\rbrace$$

再找 ，是 ：

接下来是这样：

$$\lbrace1,2,4\rbrace\lbrace3\rbrace\lbrace5\rbrace\lbrace6\rbrace\lbrace7\rbrace$$

对于 号点，这不就连到了新的 号点嘛：

又减少了一个集合：

$$\lbrace1,2,4\rbrace\lbrace3,5\rbrace\lbrace6\rbrace\lbrace7\rbrace$$

这样下去，在第一次循环里会得到两坨连通块：

现在的集合是这样了：

$$\lbrace1,2,4,6\rbrace\lbrace3,5,7\rbrace$$

在第二次循环里就只能把最后的两坨连通块弄起来了：

最终集合：

$$\lbrace1,2,4,6,3,5,7\rbrace$$

主要代码：

void Boruvka () // 最小生成树  
{
	init ();
	int merged = 0, ans = 0;
	bool update = true;
	while (update) // 还可以进行修改  
	{
		update = false;
		memset (best, 0, sizeof (best)); // 连通块中最小的边 
		// 这里确定要合并的连通块  
		for (int i = 1; i <= m; i ++) // 遍历图中的每一条边，而且使用可以将两个连通块相连的边 
		{
			if (vis[i] == true) // 如果已经连起来就跳过  
				continue;
			int fx = find (edge[i].from), fy = find (edge[i].to); // 找到边端点的连通块父亲  
			if (fx == fy) // 如果它们俩是同一个连通块就跳过  
				continue;
			if (judge (i, best[fx]) == true) // 对 x 的连通块扩展边择优 
				best[fx] = i;
			if (judge (i, best[fy]) == true) // 择 y 的连通块扩展边择优 
				best[fy] = i;
		}
		// 这里负责合并  
		for (int i = 1; i <= n; i ++)
		{
			if (best[i] != 0 && vis[best[i]] == false) // 保证上面选择的最优边符合前提  
			// 如果不存在还有边可以使不同的连通块连通，下一次就不会进入 while 
			{
				update = true; // 本次合并了 
				merged ++;
				ans += edge[best[i]].w; // 统计答案 
				vis[best[i]] = true; // 标记该边已使用  
				fa[find (edge[best[i]].from)] = find (edge[best[i]].to); // 用这条边建立父子关系  
			}
		}
	}
	if (merged == n - 1)
		printf ("%d\n", ans); 
}

时间复杂度是还可以的 。