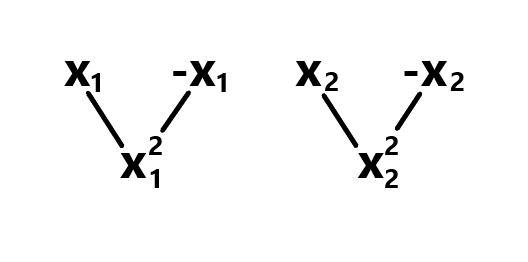我看起来像是没事一样么……但是逃避又能怎样,就算害怕,我也要战斗。——《辉夜大小姐想让我表白~天才们的恋爱头脑战》
快速傅里叶变换
快速傅里叶变换( ,是快速计算序列的离散傅里叶变换( 傅里叶分析 将信号从原始域 (通常是时间或空间)转换到频域 的表示或者逆过来转换。主要用于解决一些多项式问题(卷积)问题,很大部分的现代技术,包括无线通讯,定位系统与广阔的信号处理领域相关的东西都基于该算法。
前置芝士有矩阵、离散傅里叶变换、时域到频域转换、原根、复数、微积分、欧拉公式 等等,但是我一个都不会(真的,不是开玩笑)。
所以我们先从多项式乘法 开始讲起。
多项式 多项式乘法
然后现在我们重复应用乘法分配律来相乘多项式:
非常好用,但是很慢,然而这就是乘法的本质,卷积 。
卷积 如果现在用暴力来做多项式乘法,很轻松地得到以下方法:
设:
那么可以表达成:
也就是想要得到
同样也可以写成这样:
多项式乘法就是加法卷积,然后因为后面时间复杂度会噼里啪啦地炸开来所以就不讲了(擦汗)。
系数表达 然后有一个中朋友和大朋友能想到但是小朋友不能想到的想法就是将这个多项式的系数对应到一个序列里去:
列表中第 多项式的系数表示 。
如果存在:
这样子
我们会环着这片海走下去。或许有一天,我们会真正回到起点
点值表示 一个真正不错的想法是点值表示 。
次数为
如果想要证明,和该点集对应的有且只有一组系数,如果我们实际计算经过这些点的多项式(这就是点值表示 ):
然后我们就得到了一组方程式,就可以将其写成矩阵向量乘积来帮助分析(具体这个东西我也不是很清楚):
这里就不多加赘述了。
而我们将多项式的系数表示 转换为点值表示 ,这个炫酷的魔术,就是闻名中外的快速傅里叶变换 。
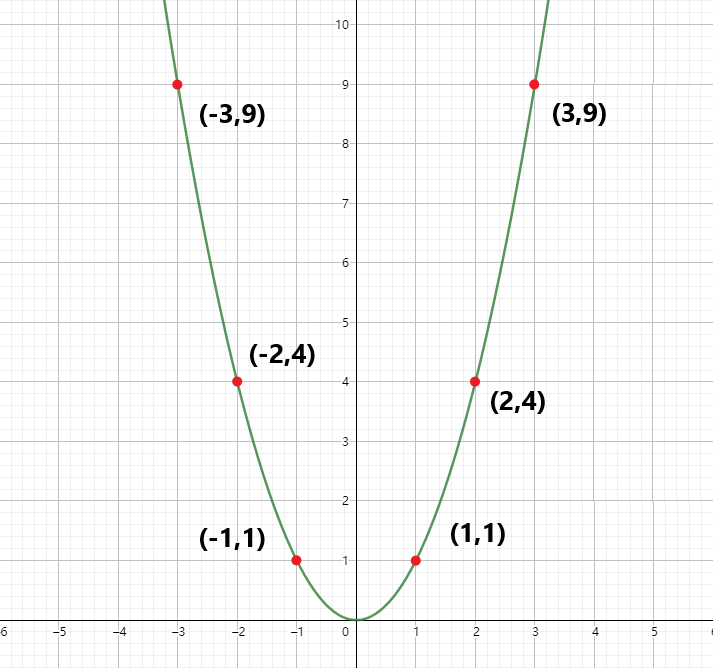
多项式求值 设我们现在有一个多项式:
选取
假设现在取一函数为 知道一个点的函数值就知道另一点的函数值 的点。
显然因为偶函数的定义
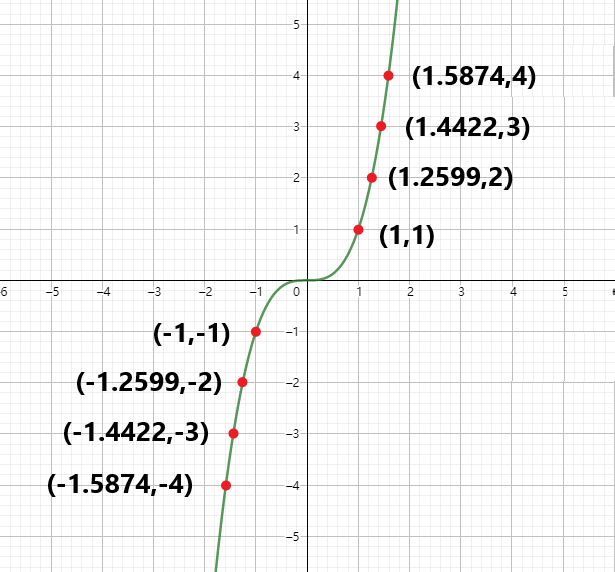
再扩展到
此时因为奇函数的性质
那么我们利用此想法扩展到更一般的多项式,对于一个多项式:
分解这个多项式:
这样可以减少我们正负点对的计算,而且还把点的数量减少到了
然后我们就得到了一个时间复杂度为
唯一可行的方法是扩展初始点的值域,所以我们引入一个不得不引入的绝对领域,复数。
复数 在了解复数 之前,首先我们要提到一个对于小朋友和中朋友很降智的问题:
诶,等等,根号里面不是不可以是负数的吗?
对于很多大朋友及以上的朋友,答案就是它了:
所以:
这玩意不是我定义的所以我也不知道(笑)。
我们把形如 复数域是实数域的代数闭包 ,即任何复系数多项式在复数域中总有根,复数域也是目前已知最大的域。在复平面中, 幅角 ,假设以逆时针为正方向 ,从
这里给出复数的代码,这份是使用重载运算符的:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 struct Complex { Complex (double xx = 0 , double yy = 0 ) {x = xx, y = yy}; double x, y; Complex operator + (Complex const &B) const { return Complex (x + B.x, y + B.y); } Complex operator - (Complex const &B) const { return Complex (x - B.x, y + B.y); } Complex operator * (Complex const &B) const { return Complex (x * B.x - y * B.y, x * B.y + y * B.x); } Complex operator / (Complex const &B) const { double t = B.x * B.x + B.y * B.y; return Complex ((x * B.x + y * B.y) / t, (y * B.x - x * B.y) / t); } } a, b;
当然也有模板类版的(由
1 typedef complex <double > comp;
单位根 上面好像只是一个广告,现在我们步入正题,假设现在有一个三阶多项式:
那么我们需要
为了递归的可行性,这两点也必须是正负对,所以
那么如果我们现在用
为了让右边等于
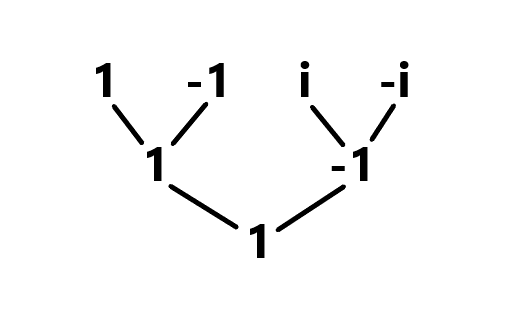
这组特殊的点就是四次单位根 (诺,就最底下的
那么如果我们有一个 单位根 。
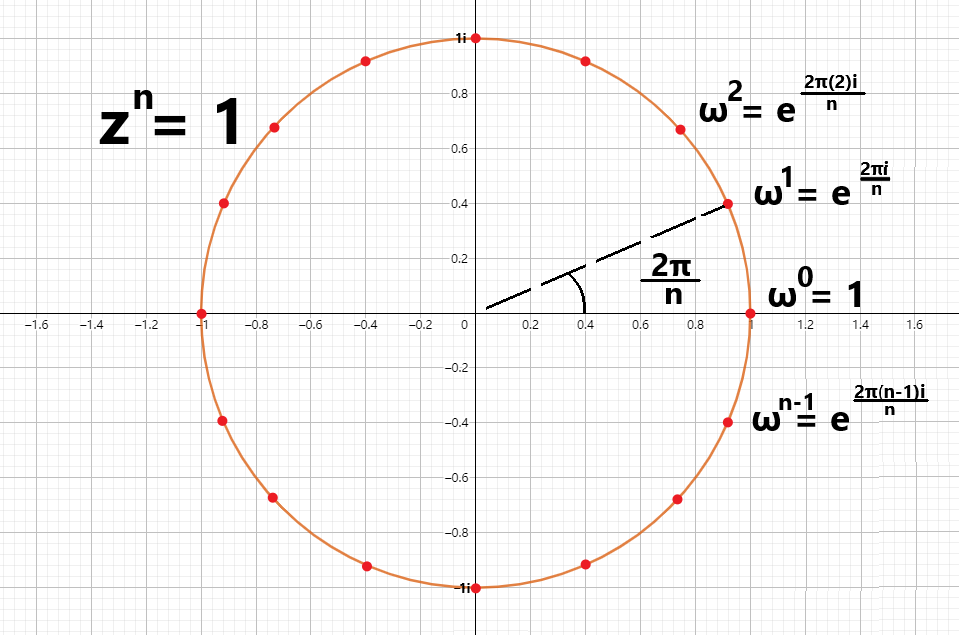
将 欧拉公式 :
这里要提到的一个东西是单位圆 ,在这里の三角函数采用弧度制,一个整圆不再是
而
如果听不懂了,没有关系,后面的你更听不懂,这样就简洁地定义了每一个
然后,当我们要计算
至于欧拉公式 ,是这么个东西(反正我是看不懂,不重要这个不是我们的重点,请感性理解,但是接下来你必须使用到它):
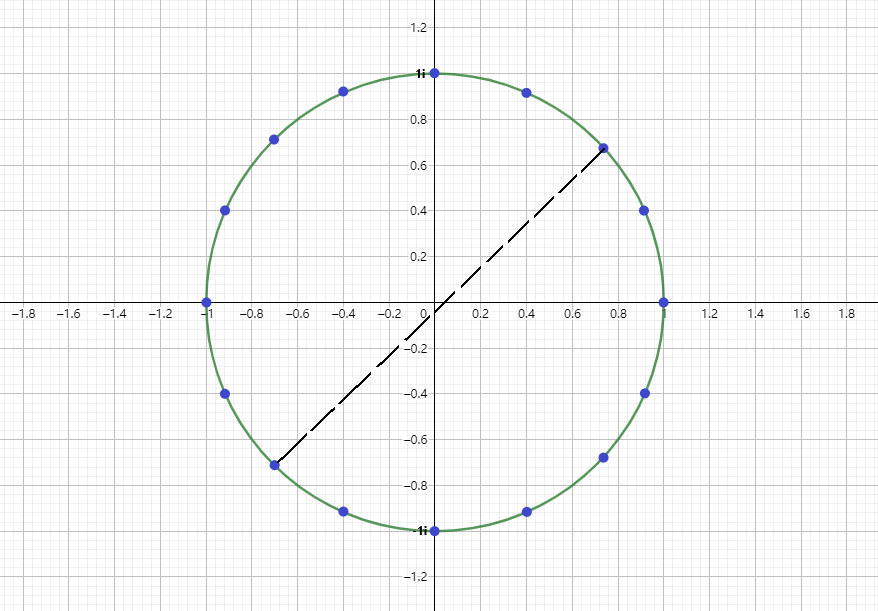
让我们回到最初的问题,为什么要在
观察上图发现,第
给出用欧拉公式求单位根的代码:
1 2 3 4 5 6 Complex sav (cos (2 * Pi / n), sin (2 * Pi / n)), buf (1, 0); for (int i = 0 ; i < n; i ++){ w[i] = buf; buf = buf * sav; }
FFT DFT 讲了那么多,让我们来理一理
先处理当
接下来,该多项式要调用
其中利用到了正负对的思想:
然后因为单位根的性质,就会产生以下关系:
如果你懵掉了的话,我们需要讲一个欧拉恒等式 :
利用单位根的性质,我们就可以把前面的第二个等式修改成:
然后,在代码里处理的时候:
最后一步了(坚持住啊,后面还有更难的在等着你!),我们要返回在
看,这不就结束了吗(真的结束了吗?),现在,我们放出简单实现的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 #include <cstdio> #include <cmath> using namespace std ;const double Pi = acos (-1 ); const int N = 1e6 + 1 ;int n, m;struct Complex { Complex (double xx = 0 , double yy = 0 ) {x = xx, y = yy;} double x, y; Complex operator + (Complex const &B) const { return Complex (x + B.x, y + B.y); } Complex operator - (Complex const &B) const { return Complex (x - B.x, y - B.y); } Complex operator * (Complex const &B) const { return Complex (x * B.x - y * B.y, x * B.y + y * B.x); } Complex operator / (Complex const &B) const { double t = B.x * B.x + B.y * B.y; return Complex ((x * B.x + y * B.y) / t, (y * B.x - x * B.y) / t); } } f[N], sav[N]; void dft (Complex *f, int len) if (len == 1 ) return ; Complex *fl = f, *fr = f + len / 2 ; for (int k = 0 ; k < len; k ++) sav[k] = f[k]; for (int k = 0 ; k < len / 2 ; k ++) { fl[k] = sav[k << 1 ]; fr[k] = sav[k << 1 | 1 ]; } dft (fl, len / 2 ); dft (fr, len / 2 ); Complex tG (cos (2 * Pi / len), sin (2 * Pi / len)), buf (1, 0); // 每次都要算单位根因为长度不同 for (int k = 0 ; k < len / 2 ; k ++) { sav[k] = fl[k] + buf * fr[k]; sav[k + len / 2 ] = fl[k] - buf * fr[k]; buf = buf * tG; } for (int k = 0 ; k < len; k ++) f[k] = sav[k]; } int main () scanf ("%d" , &n); for (int i = 0 ; i < n; i ++) scanf ("%lf" , &f[i].x); for (m = 1 ; m < n; m <<= 1 ); dft (f, m); for (int i = 0 ; i < m; i ++) printf ("(%.4lf,%.4lf)\n" , f[i].x, f[i].y); return 0 ; }
给出上面说的主要公式:
因为是分治的那种感觉,所以时间复杂度是还能算优秀的
IDFT 诶诶诶上面的话都说了,还没有结束呢,做人啊,不能拉屎拉一半,屁股让别人擦(好像有啥不对但是我不记得那句话怎么讲了,反正就是咱们还有一个烂摊子要收就对了)。
上面的东西求完以后,只是求出了一个答案的点值表达,而并非最终结果,最后一步,我们要将求出的点值表达式还原成多项式,最终完成乘法,这个过程叫做傅里叶逆变换(不妨叫它大小姐逆告白 www)
然后这里有一个非常有意思的结论(涉及单位根反演 ,也可以理解成范德蒙德矩阵求逆):
把
现在假设多项式
所以有以下式子:
结论即:
最终的一个转换是,其中
所以我们把代码改成这样:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 void idft (Complex *f, int len) if (len == 1 ) return ; Complex *fl = f, *fr = f + len / 2 ; for (int k = 0 ; k < len; k ++) sav[k] = f[k]; for (int k = 0 ; k < len / 2 ; k ++) { fl[k] = sav[k << 1 ]; fr[k] = sav[k << 1 | 1 ]; } idft (fl, len / 2 ); idft (fr, len / 2 ); Complex tG (cos (2 * Pi / len), -sin (2 * Pi / len)), buf (1, 0); for (int k = 0 ; k < len / 2 ; k ++) { sav[k] = fl[k] + buf * fr[k]; sav[k + len / 2 ] = fl[k] - buf * fr[k]; buf = buf * tG; } for (int k = 0 ; k < len; k ++) f[k] = sav[k]; }
好像没啥改变,只有一个负号。
但是因为常数太大了所以时间复杂度会膨的一下爆炸,应该是过不了模板题。
代码实现 最后这里给出最简单的代码实现,我们可以把
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 #include <cstdio> #include <cmath> using namespace std ;const double Pi = acos (-1 ); const int N = 1e6 + 5e5 + 1 ; int n, m;struct Complex { Complex (double xx = 0 , double yy = 0 ) {x = xx, y = yy;} double x, y; Complex operator + (Complex const &B) const { return Complex (x + B.x, y + B.y); } Complex operator - (Complex const &B) const { return Complex (x - B.x, y - B.y); } Complex operator * (Complex const &B) const { return Complex (x * B.x - y * B.y, x * B.y + y * B.x); } Complex operator / (Complex const &B) const { double t = B.x * B.x + B.y * B.y; return Complex ((x * B.x + y * B.y) / t, (y * B.x - x * B.y) / t); } } f[N << 1 ], p[N << 1 ], sav[N << 1 ]; void fft (Complex *f, int len, bool flag) if (len == 1 ) return ; Complex *fl = f, *fr = f + len / 2 ; for (int k = 0 ; k < len; k ++) sav[k] = f[k]; for (int k = 0 ; k < len / 2 ; k ++) { fl[k] = sav[k << 1 ]; fr[k] = sav[k << 1 | 1 ]; } fft (fl, len / 2 , flag); fft (fr, len / 2 , flag); Complex tG (cos (2 * Pi / len), sin (2 * Pi / len)), buf (1, 0); // 每次都要算单位根因为长度不同 if (!flag) tG.y *= -1 ; for (int k = 0 ; k < len / 2 ; k ++) { sav[k] = fl[k] + buf * fr[k]; sav[k + len / 2 ] = fl[k] - buf * fr[k]; buf = buf * tG; } for (int k = 0 ; k < len; k ++) f[k] = sav[k]; } int main () scanf ("%d %d" , &n, &m); for (int i = 0 ; i <= n; i ++) scanf ("%lf" , &f[i].x); for (int i = 0 ; i <= m; i ++) scanf ("%lf" , &p[i].x); for (m += n ,n = 1 ; n <= m; n <<= 1 ); fft (f, n, 1 ); fft (p, n, 1 ); for (int i = 0 ; i < n; i ++) f[i] = f[i] * p[i]; fft (f, n, 0 ); for (int i = 0 ; i <= m; i ++) printf ("%d " , (int ) (f[i].x / n + 0.49 )); return 0 ; }
提交记录:
所以我们要优化!
优化 减少计算次数 来看这一段代码:
1 2 sav[k] = fl[k] + buf * fr[k]; sav[k + len / 2 ] = fl[k] - buf * fr[k];
复数做乘法的代价是很高的,但是我们却偏偏把
所以可以改成这样:
1 2 3 Complex temp = buf * fr[k]; sav[k] = fl[k] + temp; sav[k + len / 2 ] = fl[k] - temp;
蝴蝶变换 在代码中我们使用了大量的数组拷贝,现在要通过一些歪门邪道来避免数组拷贝(标题看着很阴间但是其实还好啦)。
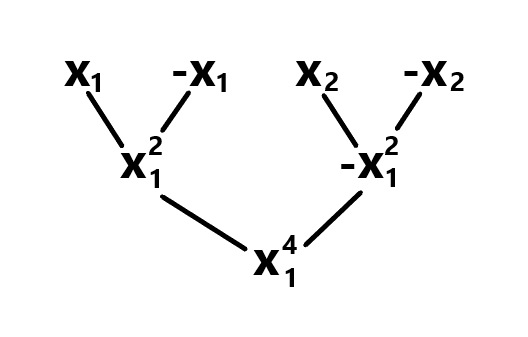
让我们用一张图来看看分治究竟在搞什么飞机:
我们要先求出最后一层的数组状况,然后才能向上合并。
然后其实你可以观察一下(反正我是没看出来),有一个小小的规律:
是不是看出来了?看不出来我也要揭秘了,再不揭秘花儿都要谢了。
可以看到 蝴蝶变换 。
如果使用
1 2 for (int i = 0 ; i < limit; i ++) tr[i] = (tr[i >> 1 ] >> 1 ) | ((i & 1 ) ? limit >> 1 : 0 );
这个过程可以类比数位
我们可以把一个二进制的反转拆成其他部分和最后一位两部分来看,其他部分的反转就是 tr[i >> 1] >> 1 ,然后判一下最后一位,如果是 limit >> 1 。
也可以这样写:
1 2 3 4 5 6 for (int i = 0 ; i < limit; i ++){ tr[i] = (tr[i >> 1 ] >> 1 ) | ((i & 1 ) << bit); if (i < tr[i]) swap (a[i], a[tr[i]]); }
迭代 因为所有位置都确定了所以可以使用迭代的写法(而且这是最经典的写法,为什么不去学 ):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 #include <bits/stdc++.h> using namespace std ;const double Pi = acos (-1 ); const int N = 1e6 + 5e5 + 1 ; int n, m;struct Complex { Complex (double xx = 0 , double yy = 0 ) {x = xx, y = yy;} double x, y; Complex operator + (Complex const &B) const { return Complex (x + B.x, y + B.y); } Complex operator - (Complex const &B) const { return Complex (x - B.x, y - B.y); } Complex operator * (Complex const &B) const { return Complex (x * B.x - y * B.y, x * B.y + y * B.x); } Complex operator / (Complex const &B) const { double t = B.x * B.x + B.y * B.y; return Complex ((x * B.x + y * B.y) / t, (y * B.x - x * B.y) / t); } } f[N << 1 ], p[N << 1 ]; int tr[N << 1 ];void fft (Complex *f, bool flag) for (int i = 0 ; i < n; i ++) if (i < tr[i]) swap (f[i], f[tr[i]]); for (int p = 2 ; p <= n; p <<= 1 ) { int len = p >> 1 ; Complex tG (cos (2 * Pi / p), sin (2 * Pi / p)) ; if (!flag) tG.y *= -1 ; for (int k = 0 ; k < n; k += p) { Complex buf (1 , 0 ) ; for (int l = k; l < k + len; l ++) { Complex tt = buf * f[len + l]; f[len + l] = f[l] - tt; f[l] = f[l] + tt; buf = buf * tG; } } } } int main () scanf ("%d %d" , &n, &m); for (int i = 0 ; i <= n; i ++) scanf ("%lf" , &f[i].x); for (int i = 0 ; i <= m; i ++) scanf ("%lf" , &p[i].x); for (m += n ,n = 1 ; n <= m; n <<= 1 ); for (int i = 0 ; i < n; i ++) tr[i] = (tr[i >> 1 ] >> 1 ) | ((i & 1 ) ? n >> 1 : 0 ); fft (f, 1 ); fft (p, 1 ); for (int i = 0 ; i < n; i ++) f[i] = f[i] * p[i]; fft (f, 0 ); for (int i = 0 ; i <= m; i ++) printf ("%d " , (int ) (f[i].x / n + 0.49 )); return 0 ; }
如果要用建议直接用这个板子,下面是提交记录:
三次变两次 我刚开始看到这个我记得不是遇到鬼的时候要三步变两步来着说……,其实是减少调用函数的次数。
根据:
假设我们要求:
设复多项式 :
那么实部就是
则:
发现
那么主函数的那块只要这样写就可以了:
1 2 3 4 5 6 fft (f, 1 ); for (int i = 0 ; i < n; i ++) f[i] = f[i] * f[i]; fft (f, 0 ); for (int i = 0 ; i <= m; i ++) printf ("%d " , (int ) (f[i].y / n / 2 + 0.49 ));
然后快了很多:
注意,如果两个多项式的值域相差太大就会卡精度。
当然求多项式还有多种方法,像
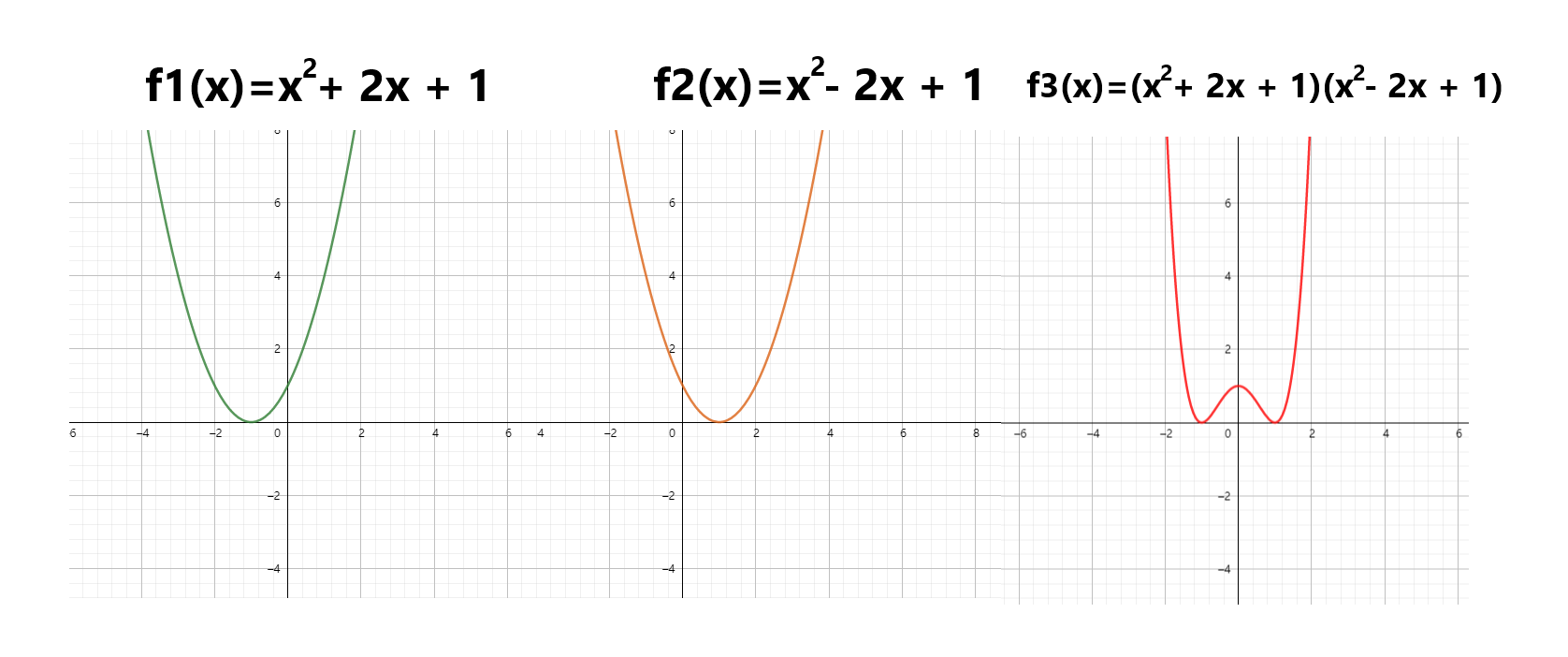 假设我们现在有两个多项式:
假设我们现在有两个多项式: