一个人总有犯错的时候，所以才需要纠错的人啊！——《恋爱研究所》

二分图

二分图，又被称作二部图、双分图和偶图，是图论中的一种特殊模型，设 是一个无向图，如果顶点 可分割为两个互不相交的子集 ，并且图中的每条边 所关联的两个顶点 和 分别属于这两个不同的顶点集 ，则称图 为二分图。

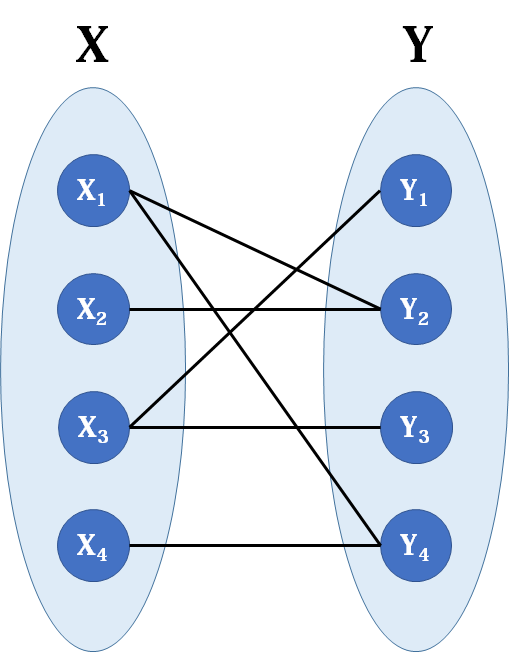
虽然我知道大家肯定都能幻想出来但是我还是要用腐朽的声音说出我是二分图

二分图判断

所以这里给出一个非常非常重要的定理，二分图充要条件是这个图里莫得奇环，如果我们把两个集合中的点分别染成黑色和白色，那么每条边的都一定连接着一个白点和一个黑点。

奇环也就是长度为奇数的环，因为每条边肯定都是从一个集合走到另一个集合，所以只有走偶数次才可能回到同一个集合。

换一种说法，在判断中，我们就要找到一种是否能把图中顶点分为两个符合条件的集合的方法，莫得那就不是了，只要我们发现奇环就说明这个图不是二分图。

想法应该很简单了，我们直接给出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool dfs (int u, int color) // 传入起点和当前起点的颜色  
{
	st[u] = color; // 染色
	for (int i = head[u]; i; i = edge[i].nxt) // 前向星遍历  
	{
		int v = edge[i].to;
		if (!st[v]) // 如果还未被染色 
		{
			if (!dfs (v, 3 - color)) // 这里把 0 当做未染色，1 和 2 当做白色和黑色 
				return false;
		}
		else if (st[j] == color) // 当前遍历到边的终点发现这俩颜色相同，根据前面的性质失败 
			return false;
	}
	return true;
}

然后在主函数里遍历每个点：

1
2
3
4
5
6
7
8
9
10
bool flag = true;
for (int i = 1; i <= n; i ++)
{
	if (!st[i]) // 对于一个还没有染色的点  
		if (!dfs (i, 1)) // 这个点开始染某个颜色  
		{
			flag = false;
			break;
		}
}

然后如果一个之后还未被染色的点，它开始染色为黑还是白其实是没有关系的。

二分图最大匹配

这是一个很实际的问题，假设我们现在有成对的男女生。

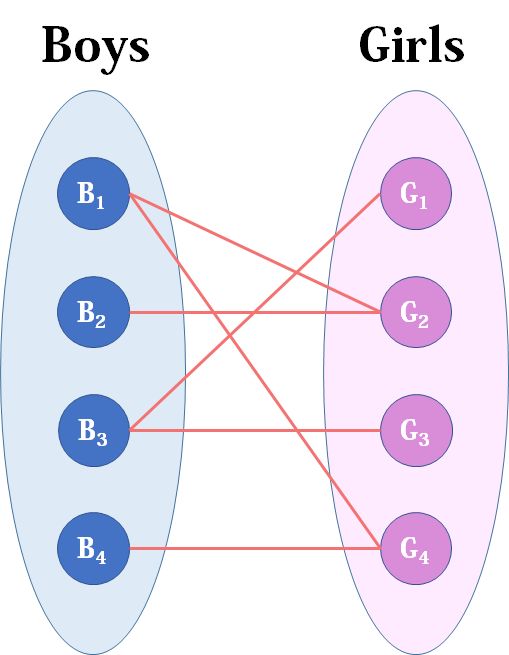
非常实际的问题……嗯对（伤心）

假设现在男生和女生们分别是两个点集，里面的点分别是男生和女生，边表示他们有些人之间存在有“暧昧关系”。最大匹配问题相当于，现在你身为红娘，可以撮合任何一对有暧昧关系的男女，那么你最多能成全多少对情侣？而数学表述就是，在二分图中最多能找到多少没有公共端点的边。

匈牙利算法/增广路算法

－

有一说一，网上对于 算法是不是匈牙利算法的异议其实很多，我个人是站在“不是但是包含”这一角度的，反正是什么说法都有，但是这并不影响我们学习它。

现在，从上面那个例子来讲匈牙利算法。

至于增广路，请悄悄悄悄悄地溜去《网络流奇谭》看看，我才不会告诉你们增广路是指从源点到汇点路径中一条交替联通两个集合的路径，其边上的流量均大于零呢。

我们从第一个男生开始看起（同样也可以从第一个女生看起），他和第二个女生有暧昧，那么我们就暂时先把他们连接起来（注意此时的安排都是暂时的）：

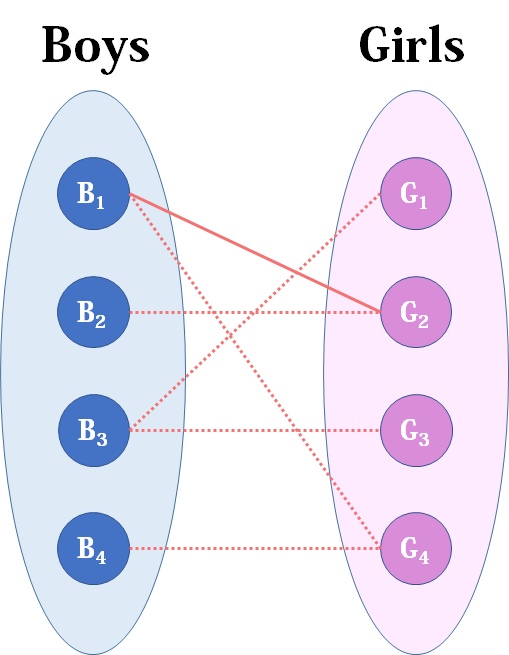
暂时安排（为什么我不是其中一员）

来看第二个男生，第二个男生也喜欢第二个女生，但此时第二个女生已经“名花有主”了（虽然是暂时安排），然后我们倒回去看给第二个女生安排的男友，是第一个男生，第一个男生有另一个选择——第四个女生，而且她还没有被安排，那么我们就给第一个男生安排上第四个女生：

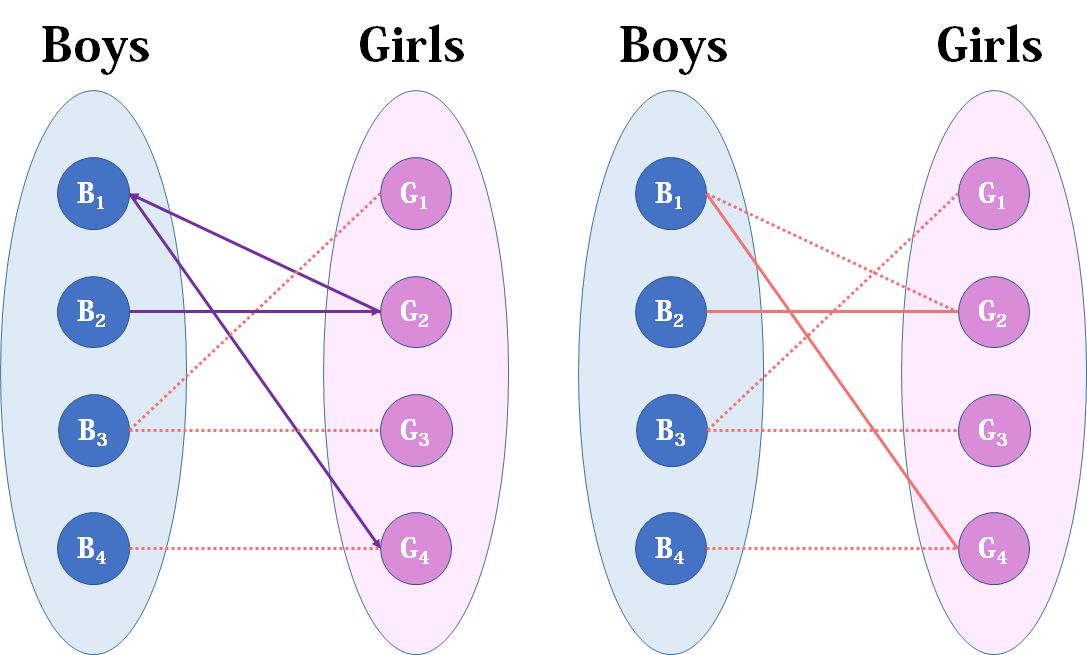
重新安排（为什么不快点来安排我）

然后看到第三个男生，直接安排第一个女生就好了，至于第四个男生，他只钟情于第四个女生，但是第四个女生目前配的是第一个男生。第一个男生除了第四个女生还可以选第二个女生，但是如果第一个男生选了第二个女生，第二个女生的原配——第二个男生就没得选了。绕了一大圈结果发现只有第四个男生和第三个女生的世界完成了。

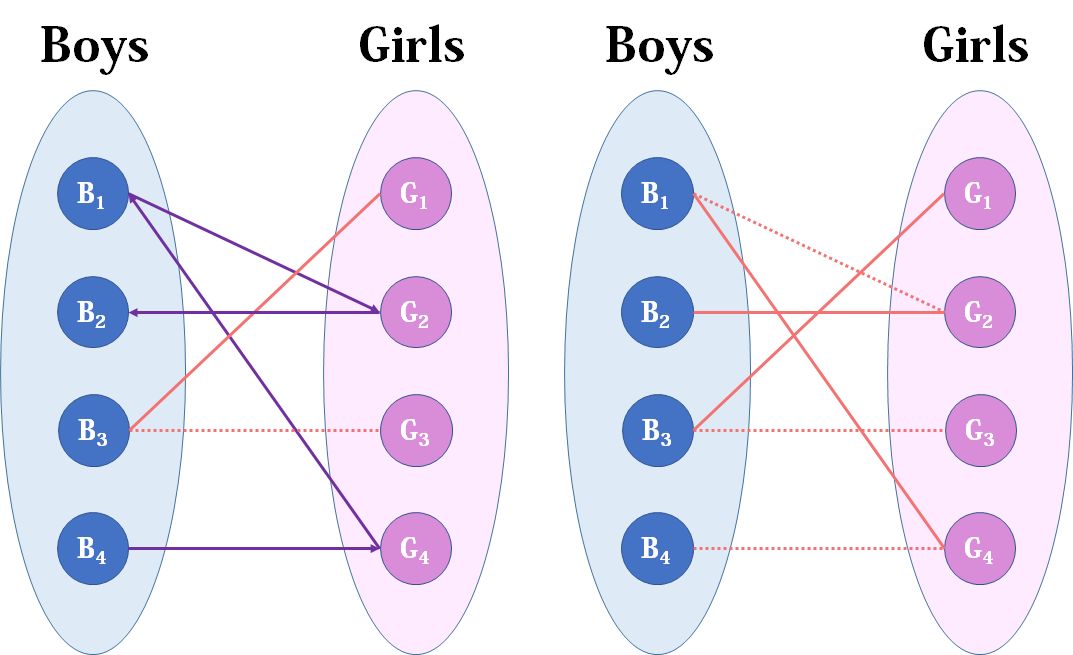
最后安排（原来我就是第三个男生）

这就是匈牙利算法的流程，让我们来看一下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int n, m; // 分别表示两个集合中元素的个数 
int mp[N][N]; // 邻接矩阵存图 
int p[N]; // 表示当前右边元素对应的左边元素 
bool vis[N]; // 记录右边元素是否被访问过  
bool match (int i)
{
	for (int j = 1; j <= m; j ++)
		if (mp[i][j] && !vis[j]) // 有边且未访问过 
		{
			vis[j] = true;
			if (p[j] == 0 || match (p[j])) // 如果暂无匹配或者原来的左侧元素可以找到新的匹配 
			{
				p[j] = i; // 当前左侧元素成为当前右侧元素的新匹配
				return true; // 返回匹配成功
			} 
		}
	return false; // 遍历完还莫得匹配，直接翘辫子了，人间孤独传说（那就是我了）
}
void Hungarian () // 匈牙利算法  
{
	int cnt = 0;
	for (int i = 1; i <= n; i ++) // 从某边开始对这个集合里的边遍历下去 
	{
		memset (vis, 0, sizeof (vis)); // 重置访问数组  
		if (match (i))
			cnt ++; // 匹配成功了一个  
	}
	return cnt;
}

时间复杂度是且得且过的 （用邻接矩阵可以优化到 ），所以我们要介绍其他算法了。

网络流算法

可以吵吵吵吵吵地爪巴去《网络流奇谭》学习各种网络流算法，然后设各种神奇的边容量为 。

（哦其实这边的神奇是我在没有意识的情况下写的所以其实我当时也不知道我自己在写什么但是你不觉得这很有意思吗所以我就保留下来了虽然可能说这句话看上去非常的不通畅啊我说上面那句话但是还是要保留下来因为有意思吧可能因为是各种神奇的边所以反正我觉得是很不流畅的不知道你是不是这么觉得呢总不可能觉得我现在写的这句话非常的没有意思吧好吧如果你真的这么觉得那我就写到这里为止了）

所有想表达的意思就是我想要一个女朋友，括号中一共有 个字。

然后还有就是实则神奇的边就是所有边，也就是多少条边能把二分图里两个集合里的点全部连起来。用 算法的话时间复杂度为 。

Hopcroft-Karp算法

匈牙利算法虽然码量小，但是时间复杂度是很糟糕的，所以有一种优化（但是码量真的很大），匈牙利算法的核心是一次只能找到一条增广路径，但是 可以一次性找到多条不相交的增广路径（就是没有公共点和公共边的增广路径），然后根据这些增广路径添加多个匹配，并逐渐增加增广路径的长度，思路和 是一样的，但是代码稍有不同，时间复杂度是 ，这边给出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
bool search_path () // 寻找增广路径集，其中每条长度是一样的  
{
	queue <int> Q;
	dis = INF;
	memset (dx, -1, sizeof (dx));
	memset (dy, -1, sizeof (dy));
	for (int i = 1; i <= n; i ++)
	{
		if (cx[i] == -1) // 未遍历的节点，入队  
		{
			Q.push (i);
			dx[i] = 0;
		}
	}
	while (!Q.empty ()) // 广度搜索增广路径  
	{
		int u = Q.front ();
		Q.pop ();
		if (dx[u] > dis)
			break;
		for (int v = 1; v <= m; v ++) // 取右侧节点  
		{
			if (mp[u][v] && dy[v] == -1) 
			{
				dy[v] = dx[u] + 1;
				if (cy[v] == -1)
					dis = dy[v];
				else
				{
					dx[cy[v]] = dy[v] + 1;
					Q.push (cy[v]);
				}
			}
		}
	}
	return dis != INF;
}
int find (int u) // 对路径集进行增广  
{
	for (int v = 1; v = m; v ++)
	{
		if (!vis[v] && mp[u][v] && dy[v] = dx[u] + 1)
		{
			vis[v] = 1;
			if (cy[v] != -1 && dy[v] == dis) 
				continue;
			if (cy[v] == -1 || find (cy[v])) // 暂无匹配或者原来的左边元素可以找到新的匹配  
			{
				cy[v] = u;
				cx[u] = v;
				return true; // 匹配成功  
			}
		}
	}
} 
int Hopcroft-Karp () // 二分图最大匹配
{
	int res = 0;
	memset (cx, -1, sizeof (cx));
	memset (cy, -1, sizeof (cy));
	while (search_path ())
	{
		memset (vis, 0, sizeof (vis));
		for (int i = 1; i <= n; i ++)
			if (cx[i] == -1) // 对于一个还未匹配的  
				res += find (i); // 进入匹配  
	}
}

最小点覆盖问题

另外一个关于二分图的问题就是求最小点覆盖，我们想找到最少的一些点，使二分图的所有边至少有一个端点在这些点中。倒过来说，删除包括这些点的边，可以删掉所有边。

看一下图就懂的：

然后解决这个问题看上去很难其实……好吧相信大家都知道我要干什么，这种难得一批的东东当然有结论啦。

König算法

一个二分图中的最大匹配数等于这个图中的最小覆盖点数。

有一个直观地找最小覆盖点集的方法，从左侧一个未匹配成功的点开始走，走一趟匈牙利算法的流程，所有左侧和右侧未经过的点，即组成最小点覆盖。

二分图最大权匹配

当然这个问题也可以用匈牙利算法解决，但是考虑到二分图中两个集合中的点并不总是相同，为了使用匈牙利算法，需要先将两个集合中点数较少的那个集合进行补点，使得两集合的点数相同，补的点权都是 ，这种情况下，就将问题转化成了求最大权完美匹配问题，从而能应用匈牙利算法解决问题。

所谓完美匹配，就是把左边的点匹配完，设 为二分图， ， 为 中一个最大匹配，且 则称 为 到 的完美匹配，通过给每个顶点一个标号（顶标）来转化问题。

给出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
bool search_path (int u) // 寻找匹配，这个过程和匈牙利算法是一样的，所以我说“包含” 
{
	for (int v = 1; v <= n; v ++)
		if (!sy[v] && lx[u] + ly[v] == mp[u][v])
		{
			sy[v] = true;
			if (match[v] == -1 || search_path (match[v]))
			{
				match[v] = u;
				return true;
			}
		}
	return false;
}
int Kuhn_Munkras ()
{
	for (int i = 1; i <= n; i ++)
	{
		ly[i] = 0; // 初始化顶标（即标号） 
		lx[i] = -0x3f;
		for (int j = 1; j <= m; j ++)
			if (lx[i] < mp[i][j])
				lx[i] = mp[i][j];
	}
	memset (match, -1, sizeof (match));
	for (int u = 1; u <= n; u ++) // 为左集合的每一个点找匹配  
	{
		while (1)
		{
			memset (sx, 0, sizeof (sx));
			memset (sy, 0, sizeof (sy));
			if (search_path (u)) // 找到了匹配，直接下一个 
				break;
			// 如果没有找到匹配，就下来修改顶标，直到找到匹配为止  
			int inc = 0x3f; // 定义一个增量， lx[i] 为搜索过的点， ly[i] 是未搜索过的点 
			for (int i = 1; i <= n; i ++)
				if (sx[i])
					for (int j = 1; j <= n; j ++)
						if (!sy[j])
							inc = min (inc, lx[i] + ly[j] - mp[i][j]); 
			for (int i = 1; i <= n; i ++)
			{
				if (sx[i])
					lx[i] -= inc; // 然后修改顶标  
				if (sy[i])
					ly[i] += inc;
			}
		} 
	}
	int sum = 0;
	for (int i = 1; i <= n; i ++)
		if (match[i] >= 0)
			sum += mp[match[i]][i];
	return sum;
}

顶标的作用就是用于判断所匹配的顶点，连成边后，是不是集合中权值比较大的边。

还有一件事，如果是最小权值，就要给整个二分图的权值取反，在最后求和的时候也要取反（这可不能忘记）。

转化为费用流模型

在图中新建一个源点和汇点，从源点向二分图的左半部分的每个点连一条流量为 ，费用为 的边，从二分图的右半部分的每个点连一条相同的边。接下来，对于每一条连接左集合的和右集合边权为 的边，则连一条从 到 的流量为 ，费用为 的边，求这个网络的最大费用最大流即可。