因为憧憬着看不到的东西，被迷惑，而迷失了那些看得到的东西，我不想这样。——《龙与虎》

再找不出一个字的算法了，只能用这个老题材了，但是发现还是有很多东西要讲……

堆

$Seak$

堆是一棵树，其每个节点都有一个键值，根据不同的堆有不同的键值存放方式。每个节点的键值都大于等于其父亲键值的堆叫小根堆，相反，每个节点的键值都小于等于其父亲键值的堆就叫大根堆（形象地记忆就是根是最大的还是最小的），大部分堆都支持插入数字，查询某个最值，删除这个最值，减小或增大某个元素的值。一些功能强大的堆还支持高效的合并操作和可持久化。

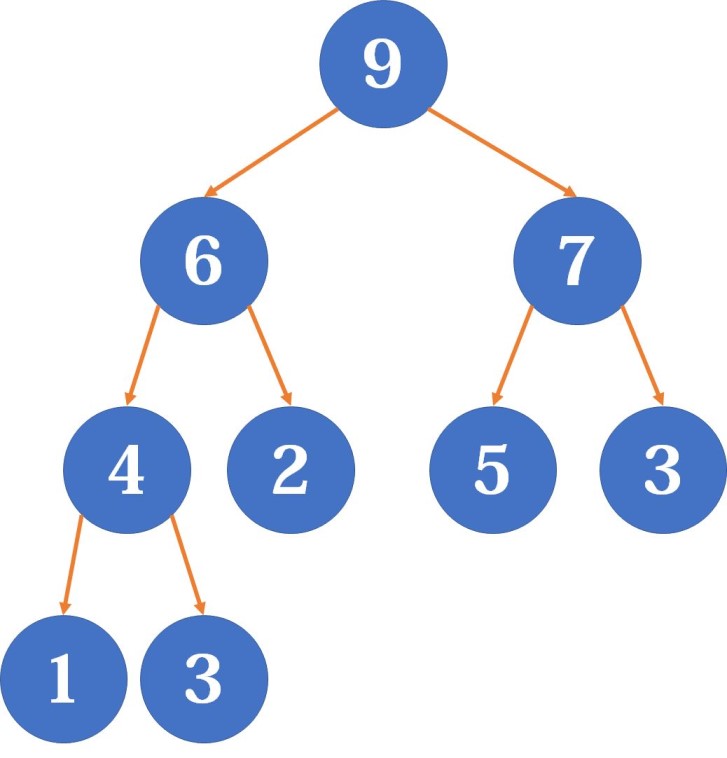
我是一个大根堆！

然后在存储的时候使用数组来储存（同样可以使用优先队列，但是手写堆更快）：

使用数组更快！更强！

习惯上来说，在提到堆的时候我们往往指下面这个堆，二叉堆。

二叉堆

二叉堆就是一棵完全二叉树，每个节点中存有一个元素。同时，它也支持很多操作（比如可持久化），接下来让我们用大根堆来举例。

上浮

既然你这么真心诚意地问了，为了防止这个二叉堆被破坏，贯彻堆与平衡的邪恶。

对于一个比自己的父节点要大的子节点，我们将两者交换，最坏情况下是从堆的最后一层浮到第一层（根），所以最多要交换 $\mathcal O(\log_2n)$ 次。

1
2
3
4
5
void swim (int n) // 上浮
{
	for (int i = n; i > 1 && heap[i] > heap[i / 2]; i /= 2) // 从堆底开始找可以交换的元素
		swap (heap[i], heap[i / 2]); // 和自己的父节点进行交换
}

下沉

我们就大发慈悲地告诉你，为了保护二叉堆的性质，可爱又迷人的反派操作。

这个操作和上浮是同理的，与较大的子节点比较，如果比它小，我们将两者交换。之所以是和较大的交换，是因为要保证换上来的子节点同样也大于另一个子节点。

1
2
3
4
5
6
7
8
9
10
void son (int n) // 获取该交换的子节点
{
	return n * 2 + (n * 2 + 1 <= size && heap[n * 2 + 1] > heap[n * 2]);
	// 如果存在右节点而且右节点比左节点大，那么就会得到 1，返回的就是右节点，反则返回左节点 
}
void sink (int n) // 下沉
{
	for (int i = n, t = son (i); t <= size && heap[t] > heap[i]; i = t, t = son (i))
		swap (heap[i], heap[t]); // 与上面的上浮同理但是只是改了改子节点的获取方式
}

建堆

我们是穿梭在银河中的二叉堆，建堆，平衡的明天在等着我们。

从一个数组 $\mathcal O(n)$ 地建立堆，复制过来然后依次下沉，因为叶子节点不需要下沉所以只需要从 $\frac{n}{2}$ 开始遍历即可。

1
2
3
4
5
6
7
void build (int A[], int n) // 建堆 
{
	memcpy (heap + 1, A, sizeof (int) * n); // 复制数组 
	size = n; // 赋值堆的大小 
	for (int i = n / 2; i > 0; i --) // 从 n / 2开始遍历  
		sink (i);
}

插入

上联：既然不知道插哪里；

下联：就直接插入到堆底；

横批：然后上浮。

感觉应该先讲插入再讲建堆的，既然为了配合火箭队的台词就算了（诶嘿嘿嘿嘿~）。

当然建堆的时候也可以一个一个插入然后插入一个就上浮一个。

1
2
3
4
5
void insert (int x) // 插入
{
	heap[++ size] = x;
	swim (size);
}

时间复杂度是还可以的 $\mathcal O(\log_2n)$ 。

删除

删除也一样（好像不是很一样），啊呀反正就是一样的，都将其弄到堆底再处理掉，这个过程就由交换直接处理，由上浮来擦屁股：

1
2
3
4
5
void pop () // 删除  
{
	swap (heap[1], heap[size --]); // 最值和堆底交换然后直接让堆的大小减一
	swim (size); // 再让其上浮一次保证性质 
}

时间复杂度是大家都一样的 $\mathcal O(\log_2n)$ 。

修改权值

修改值然后直接上浮或者下沉（随堆的性质而改变），时间复杂度是 $\mathcal O(\log_2n)$ 。

查询

直接返回根节点权值即可。

1
2
3
4
int top () // 查询 
{
	return heap[1]; // 直接返回堆顶  
}

合并

对于把两个二叉堆合并起来的脑残操作，有两种方法：

第一种就是两个堆的元素全部放一块，然后对这些元素调用 $MAKEHEAP$ _ $LIST$ （什么东西），在 $\mathcal O(n)$ 的时间内合并，大概就是一锅端了。

第二种就是遍历其中一个堆的每一个元素，调用插入函数插到另一个堆里去，需要 $\mathcal O(n\log_2n)$ 的时间，因为太慢了所以出现了二项堆这么个东西（什么东西，没事不理它反正和我们没关系），它可以在 $\mathcal O(\log_2n)$ 的时间内完成合并（什么东西）。

对顶堆

这是一个非常让人难以理解的名字，但是它的组成却很简单，就是一个大根堆和一个小根堆，将所以权值存在两个堆里来查询某个中间的值。可以小根堆的堆顶作为分界线，如果大于它就加入大根堆，如果小于它就加入小根堆。

用优先队列来实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <bits/stdc++.h>

using namespace std;

priority_queue <int, vector <int>, greater <int> > q; // 小根堆  
priority_queue <int, vector <int>, less <int> > Q; // 大根堆 

inline void pre () // 维护两个堆  
{
	while (Q.size () > q.size ()) // 把一个堆的堆顶，转移到另一个的堆底 
	{
		q.push (Q.top ());
		Q.pop ();
	}
	while (Q.size () + 1 < q.size ()) // 每个堆都是这样，享受过提心吊胆 
	{
		Q.push (q.top ());
		q.pop (); 
	}
	// 这改词好阴间  
}

int main ()
{
	scanf ("%d", &t);
	while (t --)
	{
		while (1)
		{
			scanf ("%d", &x);
			if (x == 0) // 烧完堆内元素换两个新堆  
			{
				while (!q.empty ())
					q.pop ();
				while (!Q.empty ())
					Q.pop ();
				i = 0;
				break;
			}
			if (x == -1)
			{
				if (i & 1)
				{
					printf ("%d\n", q.top ());
					q.pop ();
				}
				else
				{
					printf ("%d\n", Q.top ());
					Q.top ();
				}
				i --;
			}
			else
			{
				if (q.empty () || x > q.top ())
					q.push (x);
				else
					Q.push (x);
				i ++;
			}
			pre ();
		}
	}
	return 0;
}

可删除堆

上面那些是可合并的堆，但是现在我们要删除堆的任意一个值，就需要新建一个垃圾桶，把需要删除的值也也放进去，等到两个堆的堆顶相同时就删掉就可以了，给出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
priority_queue <int> heap, del;
inline void pre ()
{
	while (!del.empty () && heap.top () == del.top ()) // 在垃圾桶清空之前找到这个值  
	{
		heap.pop ();
		del.pop ();
	}
}
inline void push (int x)
{
	heap.push (x);
}
inline void erase (int x)
{
	del.push (x);
}

inline int top ()
{
	pre ();
	return heap.top ();
}

左偏树

这已经进化到树了，已经不是堆了……

左偏树是一种比较常用的可并堆，先给出一张狗屁概念图（其实我都很懵，这不就是树吗）：

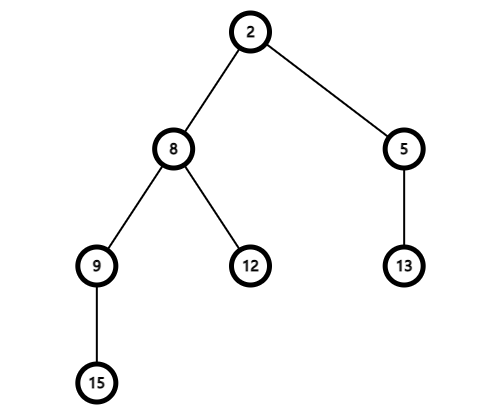
我是一棵左偏树！

既然是棵歪脖子树，我们就要解释解释为什么它是一棵歪脖子树。

定义

我们定义外节点是一个只有一个儿子或没有儿子的节点，即左右儿子至少有一个为空节点的节点。看到上面那张图，可以轻松的辨认出 $5$ 号、 $13$ 号、 $12$ 号、 $9$ 号和 $15$ 号就是外节点。

定义距离就是一个节点到离它最近的外节点的距离，即两节点之间路径的权值和。特别的，外节点的距离为 $0$ ，空节点的距离为 $-1$ 。

定义左偏树为一种满足歪脖子性质的堆有序二叉树（你看这不就是树了吗），而这歪脖子就体现在左儿子的距离不小于右儿子的距离。歪脖子树的距离就是根的距离，对于上面这棵树，树的距离就是 $2$ 到 $5$ 的距离。

如果你观察得更仔细，你就会发现对于任意节点，其距离就等于它的右儿子的距离加一。

合并

合并是左偏树的招牌操作，将两个要合并的节点丢进函数，吐出来的就是合并后的根节点。

假设我们有两个元素 $x$ 和 $y$ ，保证 $x$ 的权值小于 $y$ 。我们用递归实现，以小根堆为例，首先将根较小的一棵树作为基础，取它的右子树跟另外一棵树合并，但是在这个过程中要注意的是要保持堆的性质，即若左儿子的距离小于右儿子，则交换左右儿子。

需要注意的一个地方就是因为 $x$ 的右子树的距离可能会变所以我们根据性质来更新 $x$ 的距离。

给出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int merge (int x, int y) // 合并
{
	if (x == 0) // 如果是空节点
		return x;
	if (y == 0)
		return y;
	if (val[x] > val[y] || (val[x] == val[y] && x > y)) // 假设 x < y
		swap (x, y);
	son[x][1] = merge (son[x][1], y); // 合并
	fa[son[x][1]] = x;
	if (dis[son[x][0]] < dis[son[x][1]])
		swap (son[x][0], son[x][1]); // 保持性质然后交换
	dis[x] = dis[son[x][1]] + 1; // 通过右节点保持节点性质
	return x; // 返回一个根节点
}

时间复杂度是还可以的 $\mathcal O(\log_2n)$ 。

插入

即为一个单点左偏树和一个左偏树合并，代码如下：

1
2
3
4
5
void insert (int x, int a) // 插入
{
	int b = build ();
	a = merge (a, b);
}

时间复杂度是 $\mathcal O(\log_2n)$ 。

删除根节点

重置左右儿子的父亲，然后合并左右子树即可，代码如下：

1
2
3
4
5
6
inline void delroot (int x) // 删除根节点
{
	val[x] = -1; // 有时权值好像不用重置
	fa[son[x][0]] = fa[son[x][1]] = 0; // 重置父亲
	merge (son[x][0], son[x][1]); // 合并左右子树
}

时间复杂度是 $\mathcal O(\log_2n)$ 。

删除任意节点

前面我们也知道了，在堆里没有快速快速查找某值的位置，除非你有抽到三十块以上彩票或者用随机数 $ak$ 模拟赛的运气，不然不可能一抽就能抽到堆里的那个值，但是如果我们知道了一个位置，我们考虑删除该位置的点，先合并左右子树，把合并后的左偏树挂到这个点上，但是因为可能不保持性质所以要从这个点开始一层层下去检查并交换左右子树。

说了这么多，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
inline void delet (int x) // 删除任意节点  
{
	int p = merge (son[x][0], son[x][1]);
	fa[p] = fa[x];
	val[x] = -1;
	for (int i = fa[x]; i; i = fa[i])
	{
		if (dis[son[i][0]] < dis[son[i][1]]) // 保持歪脖子性质 
			swap (son[i][0], son[i][1]);
		if (dis[i] == dis[son[i][1]] + 1) // 保持节点距离，这个上面同样有  
			return ;
		dis[i] = dis[son[i][1]] + 1;
	} 
}

建树

一种方法是一个一个的插入，我们考虑使用优先队列优化，从队列中取出两个元素，合并后插入队尾，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void build () // 建树 
{
	queue <int> q;
	for (int i = 1; i <= n; i ++)
		q.push (i);
	int x, y;
	while (q.size ())
	{
		x = q.front (); // 娶一个斯卡蒂 
		q.pop (); // 每人一个不能多娶
		y = q.front (); // 娶一个凯尔希 
		q.pop (); // 每人一个不能多娶
		q.push (merge (x, y)); // 好了这个池子你毕业了  
	}
}

时间复杂度是 $\mathcal O(n)$ 。

总结

这里其实就是给出常用堆的各项操作的时间复杂度：

操作/数据结构 配对堆 二叉堆 左偏树 二项堆 斐波那契堆
插入 $\mathcal O(1)$ $\mathcal O(\log_2n)$ $\mathcal O(\log_2n)$ $\mathcal O(1)$ $\mathcal O(1)$
查询堆顶 $\mathcal O(1)$ $\mathcal O(1)$ $\mathcal O(1)$ $\mathcal O(\log_2n)$ $\mathcal O(1)$
删除堆顶 $\mathcal O(\log_2n)$ $\mathcal O(\log_2n)$ $\mathcal O(\log_2n)$ $\mathcal O(\log_2n)$ $\mathcal O(\log_2n)$
合并 $\mathcal O(1)$ $\mathcal O(1)$ $\mathcal O(1)$ $\mathcal O(\log_2n)$ $\mathcal O(1)$
减小一个元素的值 $\small \Omega(\log_2\log_2n) \mathcal O(\log_2n) \mathcal O(2^{2\sqrt{\log_2\log_2n}})$ $\mathcal O(\log_2n)$ $\mathcal O(\log_2n)$ $\mathcal O(\log_2n)$ $\mathcal O(1)$
是否支持可持久化 $\times$ $\checkmark$ $\checkmark$ $\checkmark$ $\times$

因为配对堆、斐波那契堆和二项堆真的太难了所以放弃了，但是它们的时间复杂度都是还算优秀的（除了二项堆）。

栈

$Htacp$

栈（ $zh\grave{a}n$ ）是一种常用的数据结构，你可以把它想象成一个垃圾桶，因为它是先进后出（ $Last\ In\ First\ Out$ ）表，简称 $LIFO$ 表。

我们可以用一个数组来模拟栈：

1
int stk[N];

当然我们的老朋友 $STL$ 也给我们提供了一个不错的模板：

1
std::stack

普通栈

压入元素

这里很简单，唯一可以优化的地方就是可以用数组的那个第零个位置（什么东西）来记栈内元素个数。

1
stk[++ stk[0]] = var; // 同样可以使用 *stk
1
var = s.push ();

取栈顶

就是当前栈内最上面的垃圾（好像是废话），注意越界问题：

1
int cur = stk[stk[0]]; 
1
int cur = s.top ();

清空

像极了寝室里一周没倒的垃圾全部倾倒在地板上的时候的快感（真的不是恐惧吗）：

1
2
while (stk[0])
	stk[0] --;
1
2
while (!s.empty ()) // 同样可以是 s.size ()
	s.pop ();

用一些简单的运算符可以比较两个栈的字典序。

单调栈

单调栈是一种和单调队列类似的数据结构。单调栈主要用于在 $\mathcal O(n)$ 的时间复杂度解决 $NGE$ （ $Next\ Greater\ Element$ ）问题，也就是对序列里每个元素，找到下一个比它大的元素。

我们维护一个栈，表示“待确定 $NGE$ 的元素”，然后遍历序列，当我们碰到一个新元素，我们知道越靠近栈顶的元素离新元素越近。所以不断比较新元素与栈顶元素，如果新元素比栈顶大，则可断定新元素就是栈顶的 $NGE$ ，于是弹出栈顶并继续比较，直到新元素不比栈顶大，再将新元素压入栈。显然，这样形成的栈是单调递增的。

模板代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
vector <int> v (n + 1), ans (n + 1);
for (int i = 1; i <= n; i ++)
	scanf ("%d", &v[i]);
stack <int> s;
for (int i = 1; i <= n; i ++)
{
	while (!s.empty () && v[s.top ()] < v[i])
	{
		ans[s.top ()] = i;
		s.pop ();
	}
	s.push (i); 
}
for (int i = 1; i <= n; i ++)
	printf ("%d ", ans[i]);

$\large End.$