服从血之盟约,与我一同奏响魂之共鸣……!——《偶像大师 灰姑娘女孩》
强连通分量
对于一张有向图而言,它是强连通( )的当且仅当其上每两个顶点都相互可达。强连通图类似于嵌套的环,而且强连通图一定有环,但 个节点的强连通图不一定有 元环。
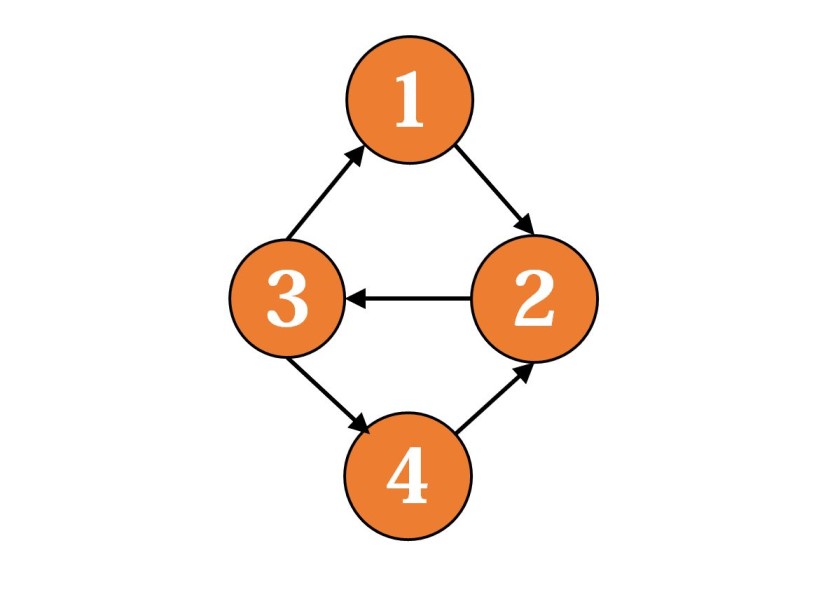
然后我们的主角,强连通分量是有向图的极大的强连通子图,“极大”意味着,把图划分为若干个强连通分量后,不存在两个强连通分量相互可达。
Kosaraju
我们需要有一个转置图,即将有向图 中的每一条边反向后形成的图称为 的转置 。
然后通过两次 ,来实现这个算法:
第一次 ,选取任意顶点作为起点,遍历所有未访问过的顶点,并在回溯之前给顶点编号,也就是后序遍历。
第二次 ,对于转置图,以标号最大的顶点作为起点开始 。这样遍历到的顶点集合就是一个强连通分量。对于所有未访问过的节点,选取标号最大的,重复上述过程。
两次 结束后,强连通分量就找出来了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| void dfs1 (int u)
{
vis[u] = true;
for (int v : g[u])
if (!vis[u])
dfs1 (v);
s.push_back (u);
}
void dfs2 (int u)
{
color[u] = cnt;
for (int v : gt[u])
if (!color[v])
dfs2 (v);
}
void Kosaraju ()
{
cnt = 0;
for (int i = 1; i <= n; i ++)
if (!vis[i])
dfs1 (i);
for (int i = n; n >= 1; i --)
if (!color[s[i]])
{
cnt ++;
dfs2 (s[i]);
}
}
|
时间复杂度是且得且过的 ,但是常数比较糟糕,所以我们要介绍下面的算法了。
Tarjan
dfs生成树
处理强连通分量的一个有力工具就是dfs 生成树,在 s 的时候,每当通过一条边 访问到一个新节点 ,就加入这个点和这条边,最后得到的便是 生成树,例如对于下面的这张有向图:
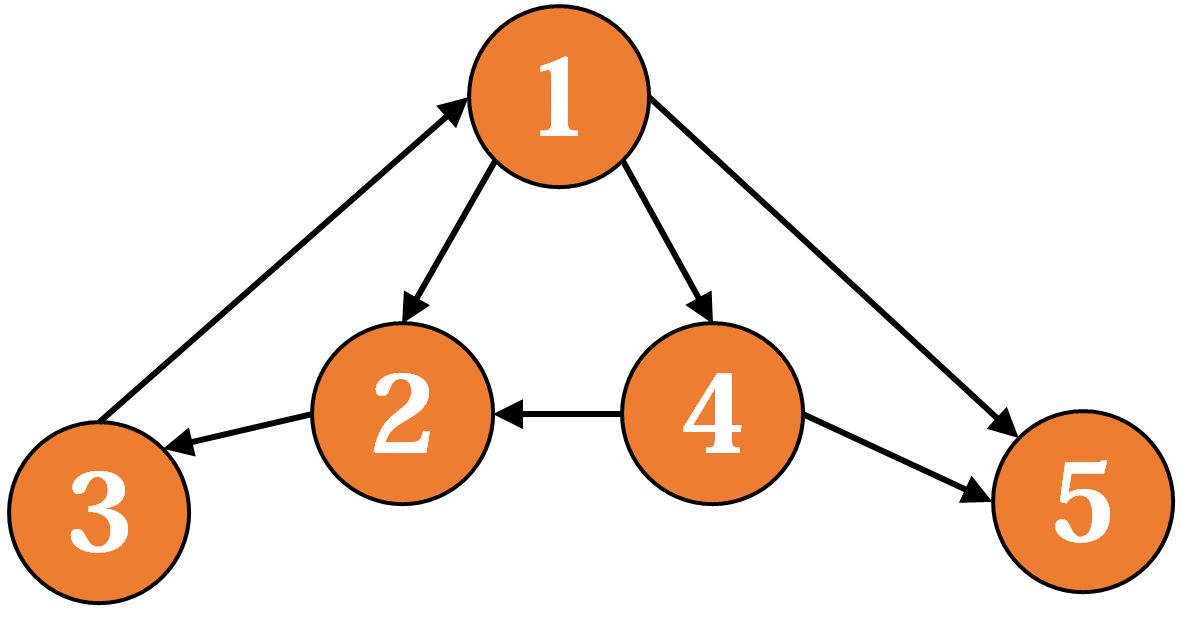
它的 生成树可能是这样(黑色实线):
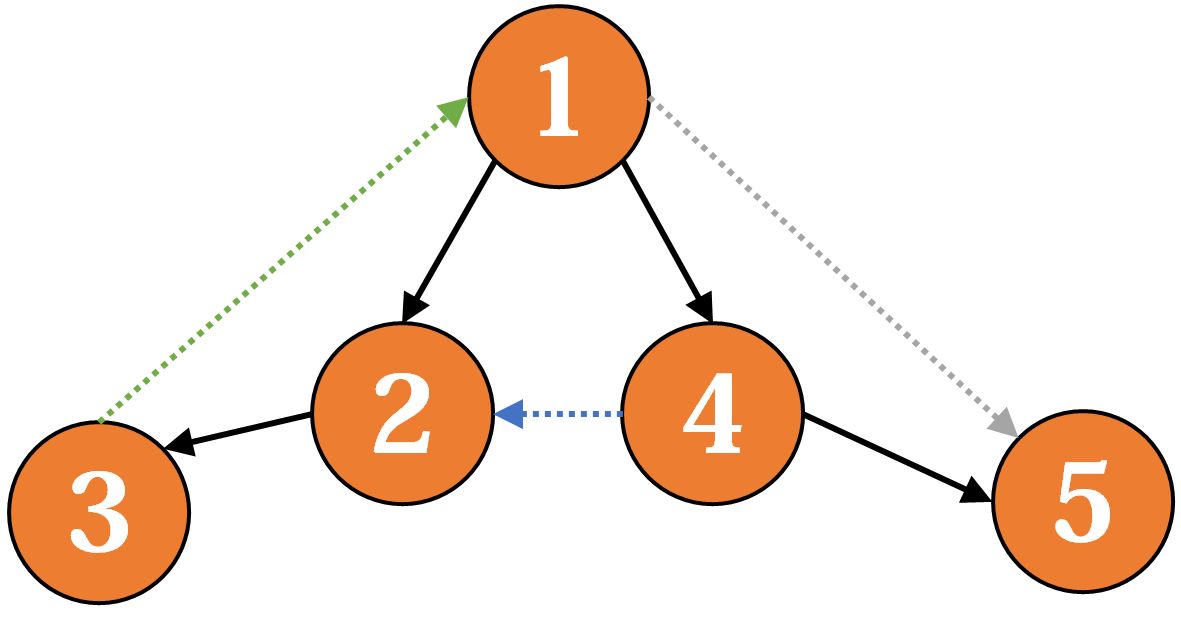
除了生成树的树边(黑色实线)以外,这里还有一些边:
1、前向边(上图灰色虚线):从某个点到它的某个子孙节点的边,这种边相当于提供某种“捷径”,在这个问题里不太重要,即使把它们全部删去也对连通性没有什么影响。
2、反向边(上图绿色虚线):从某个点到它的某个祖先节点的边。这种边就是产生环的原因,如果删去所有的反向边,那么原图会成为有向无环图,有时也叫做返祖边。
3、横叉边(上图蓝色虚线):从某个点到一个既非它子孙节点、也非它祖先节点的边。这种边本身不产生环,但是它可能把两个强连通子图”连接“起来,形成一个更大的强连通子图。
反向边和横叉边都有一个特点:起点的 序必然大于终点的 序。
这可以导出一个有用的结论:对于每个强连通分量,存在一个点是其他所有点的祖先。若不然,则可以把强连通分量划分成 个分支,使各分支的祖先节点互相不为彼此的祖先,这些分支间不能通过树边相连,只能通过至少 条横叉边相连,但这又会违背上一段话的性质。

我们把这个唯一的祖先节点称为强连通分量的根。显然,根是强连通分量中 序最小的节点。
食用
首先我们定义 定 义为 所在子树的节点经过一条非树边 (其中 可到达 )能到达的节点中最小的 序,根据这样的定义,某个点 是强连通分量的根,等价于 。我们这里必须强调 可达 ,否则在下图中,会使 ,但它实际应是一个强连通分量的根。

如果你听不懂呢,你可以将其理解成一个环,对于一个点的 就是它最早能到达的那个点的 序。
可以通过动态规划得到,对于以某个点 为起点的边 :
1、如果 未访问过,则 在 所在的子树上,如果某节点 从 起可以经过最多一条反向边到达,则从 起也可以(先从 到 ,再到 ),于是先递归处理点 ,然后令 。
2、如果 已访问过,且从 可以到达 ,则令 。
3、如果 已访问过,且从 不能到达 ,则不做任何操作(对于后两种情况都是非树边)
现在要确定一个点是否能到达另一个点,因为反向边和横叉边都指向 序较小的节点,而前向边的存在又不影响状态转移方程,所以只需要确认比该点 序小的哪些点能到达该点即可,这可以用一个栈来维护。
每当搜索到一个新点,就令它入栈。在对点 的搜索结束时,如果 ,设 s 序为 的点为 ,则 点可达的点 都可达,考虑到对 点的搜索很可能还没有结束,所以 应当留在栈中。而如果发现 满足 ,则说明 点是某个强连通分量的根,它和栈中的子孙节点相互可达。但同时,它和栈中的子孙节点也无法到达 的祖先节点,以及祖先节点其他尚未搜索的分支了,所以不断从栈顶弹出元素,直到弹出 (这样维护的栈中节点的 序是单调递增的,同时记录答案。
让我们来模拟一下:
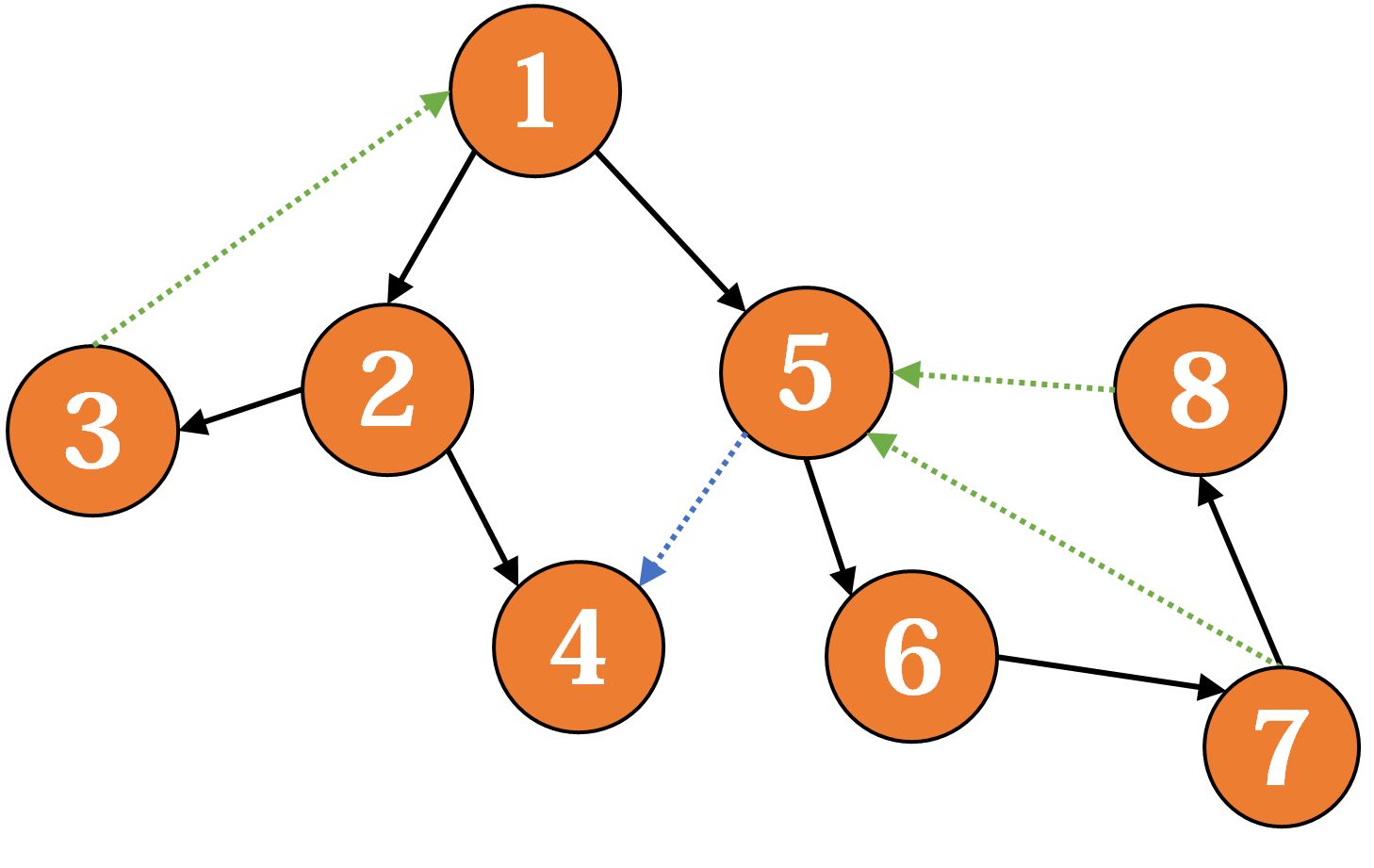
我们沿着 搜索(节点右上角表示当前的 ,下方为栈)
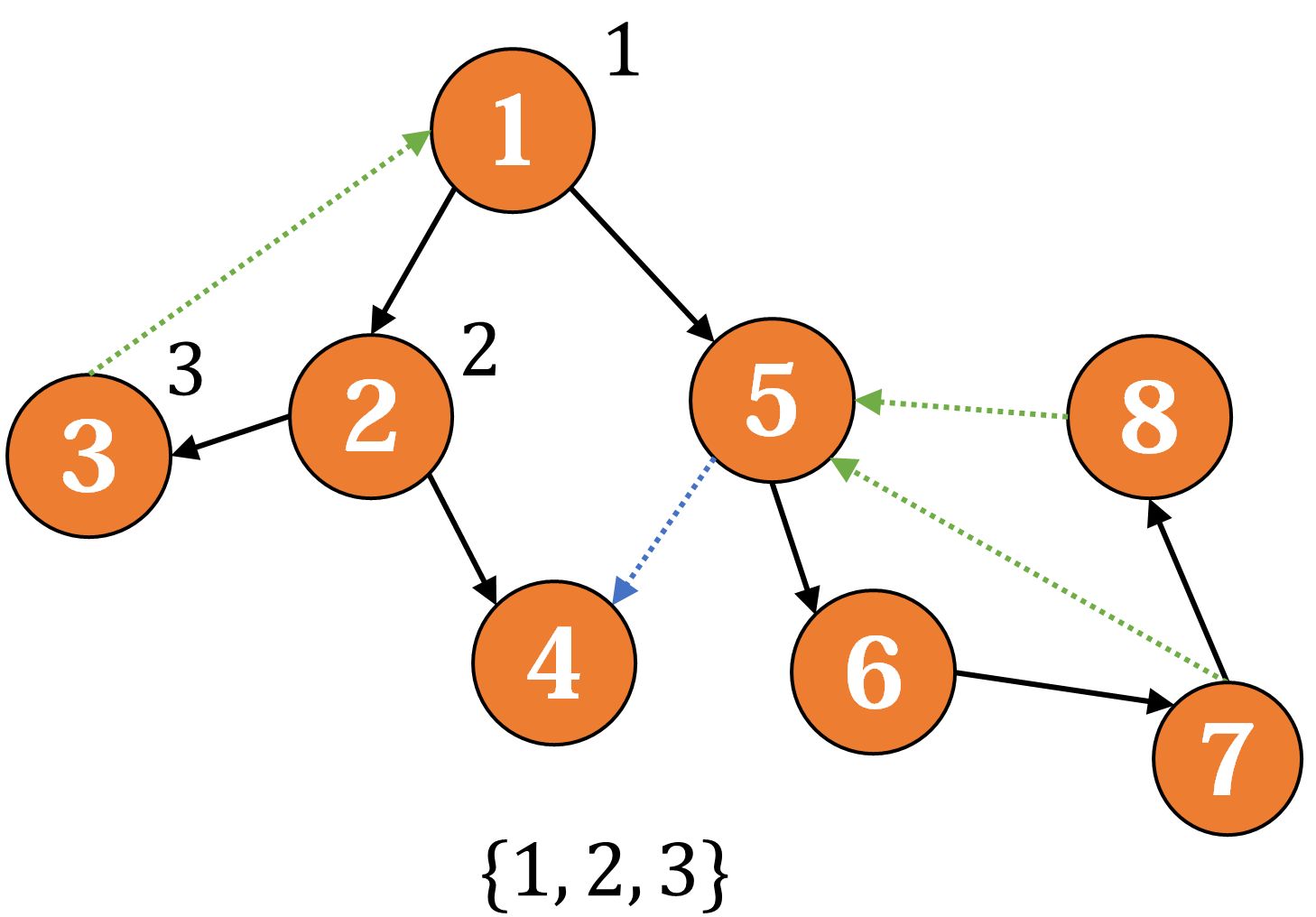
然后我们发现反向边 ,更新 ,然后回到 ,去搜索 :
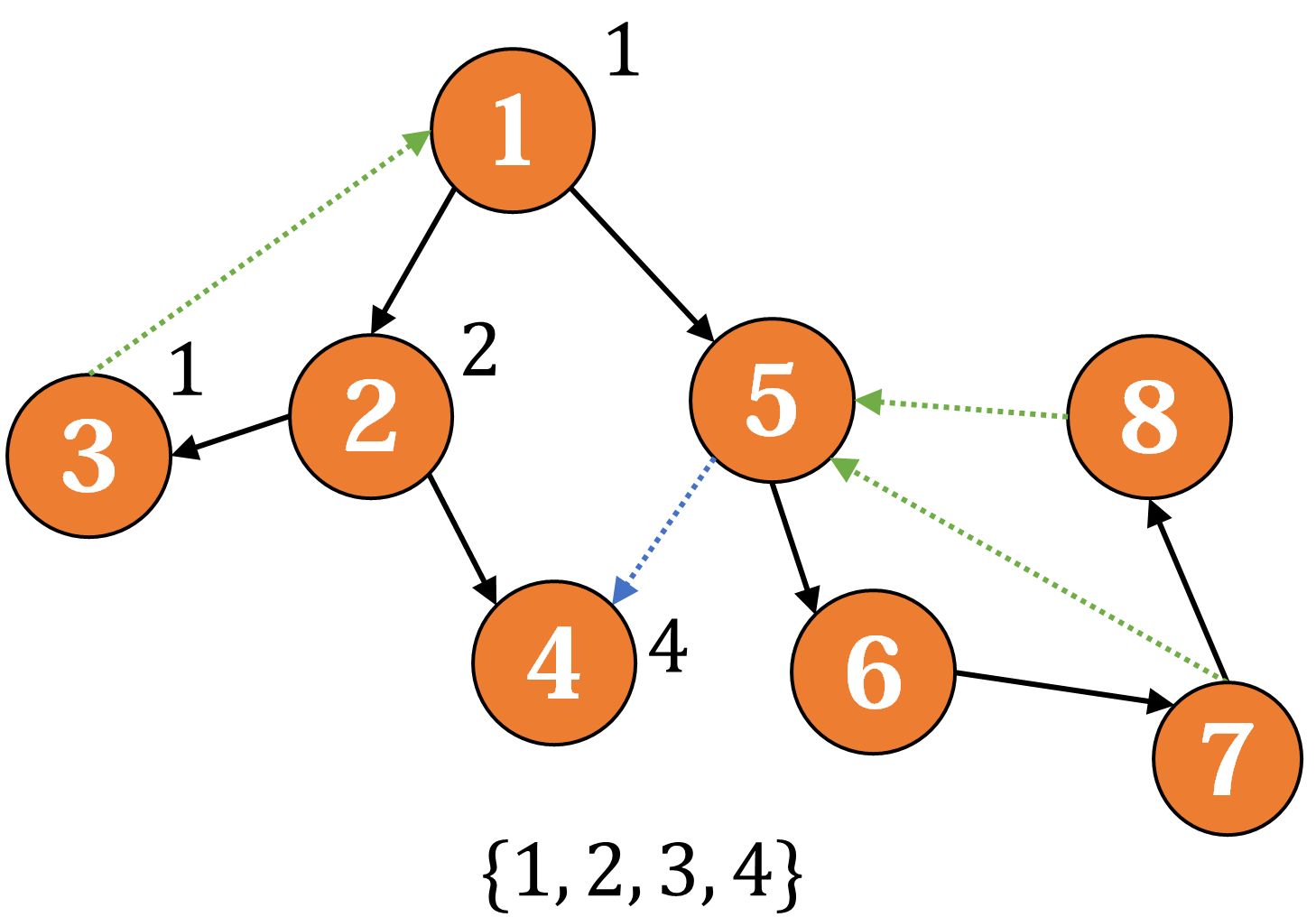
没有出边,返回,这时发现 ,于是出栈,标记它属于第一个强连通分量。
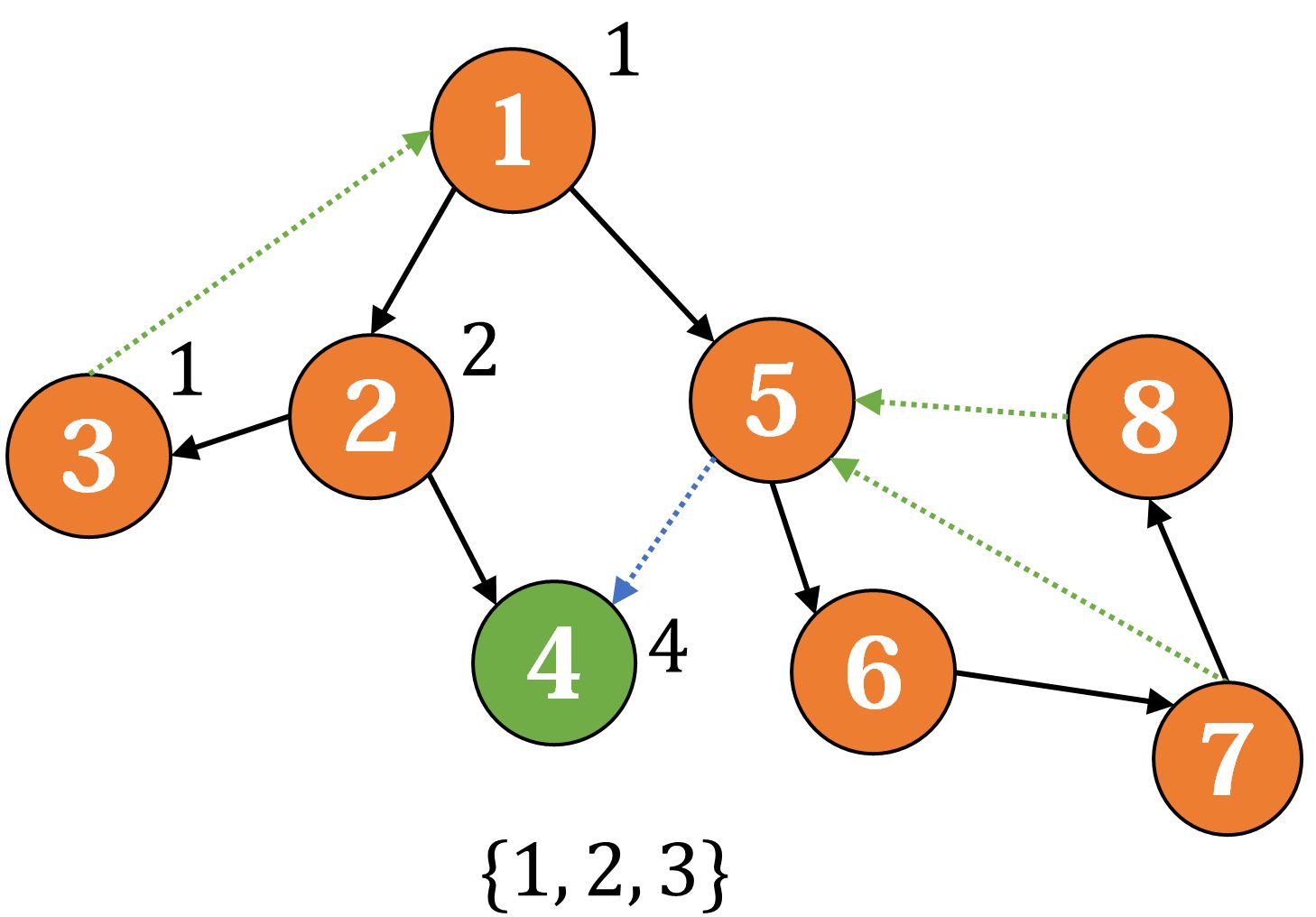
然后我们回到 ,发现它的子树已搜索完毕,更新 ;接下来搜索 :
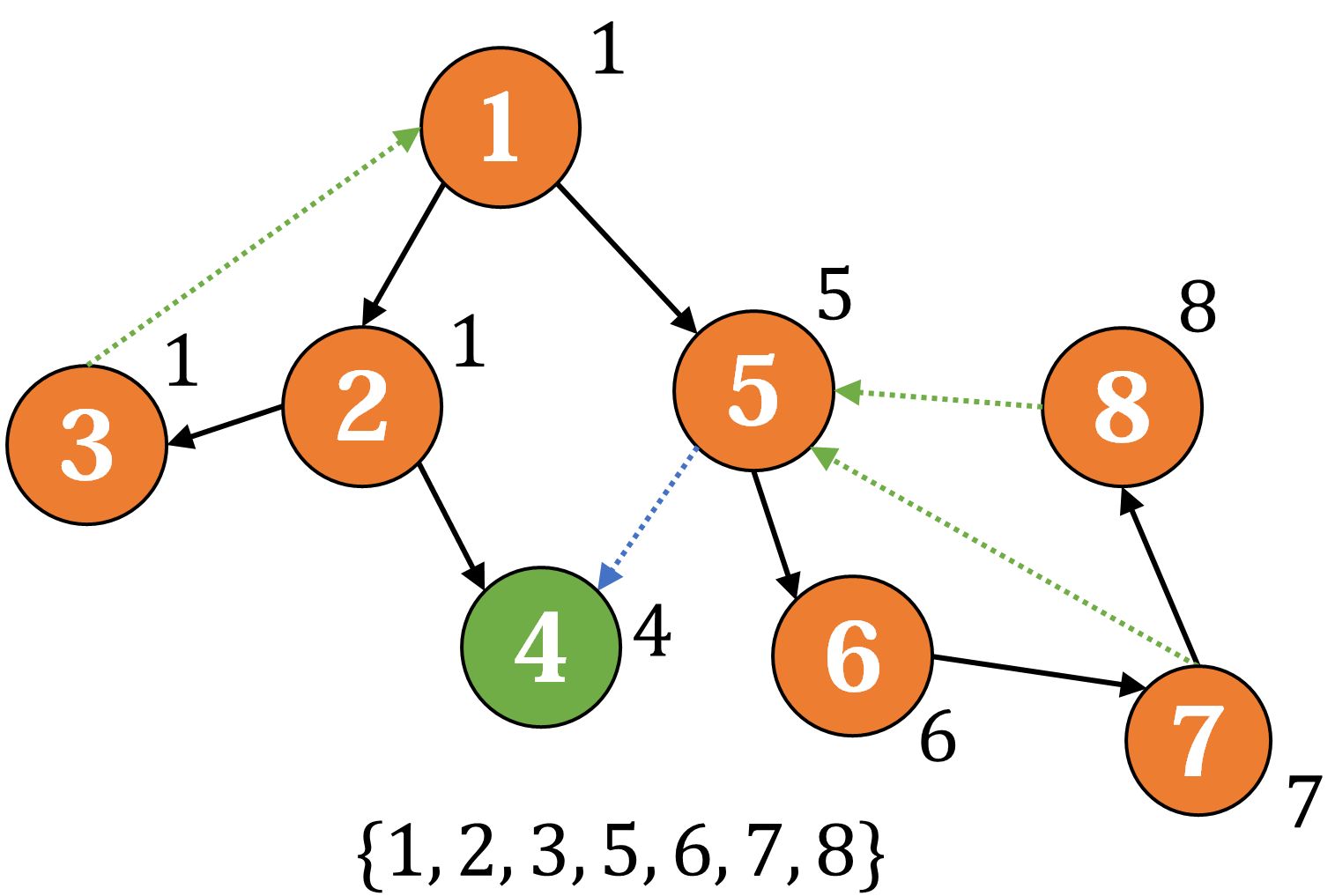
反顺序更新它们的 ,到 时发现有 ,于是把它们归入一个新的强连通分量:
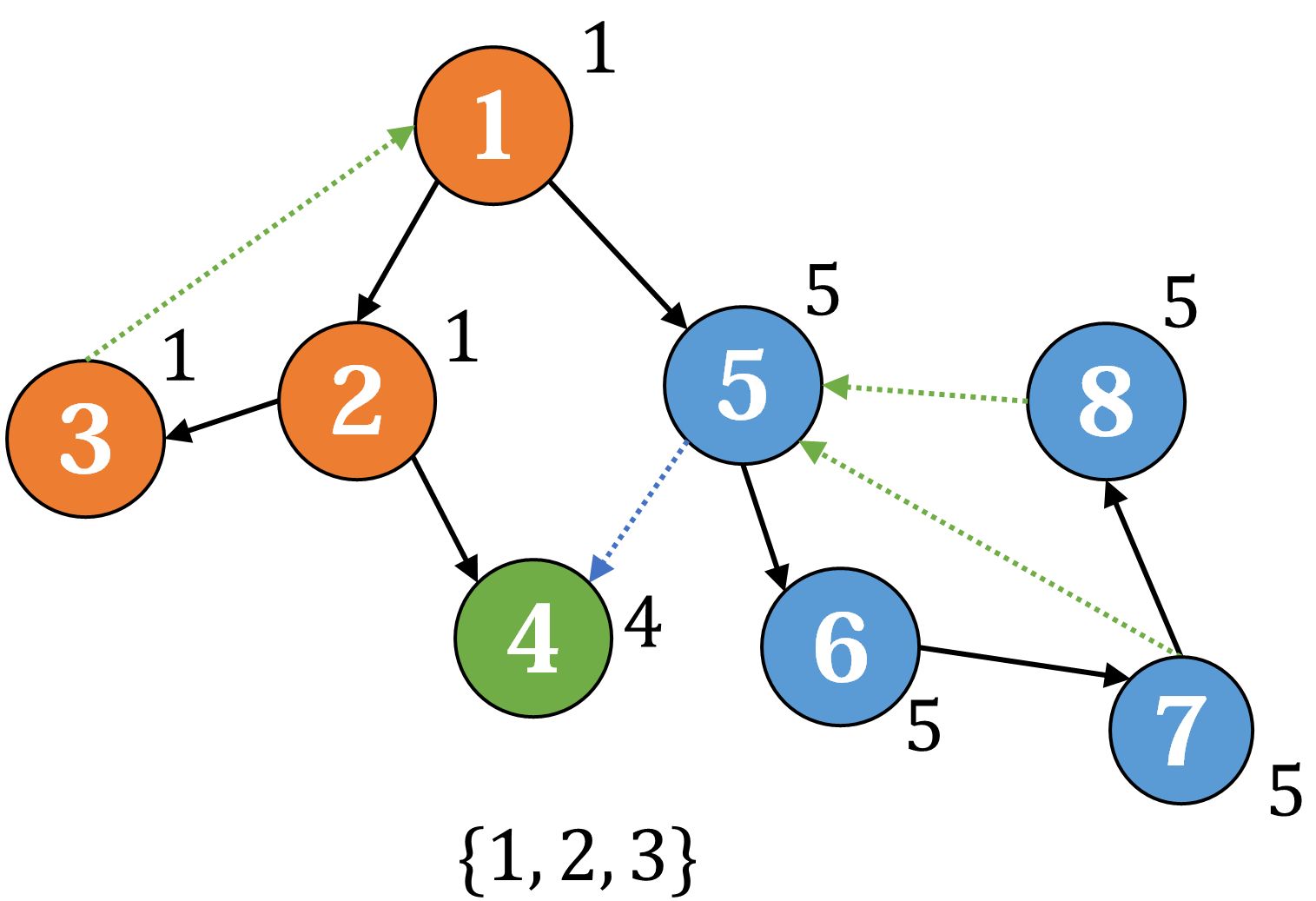
最后回到 ,把剩下还在栈内的节点都归入最后一个强连通分量:
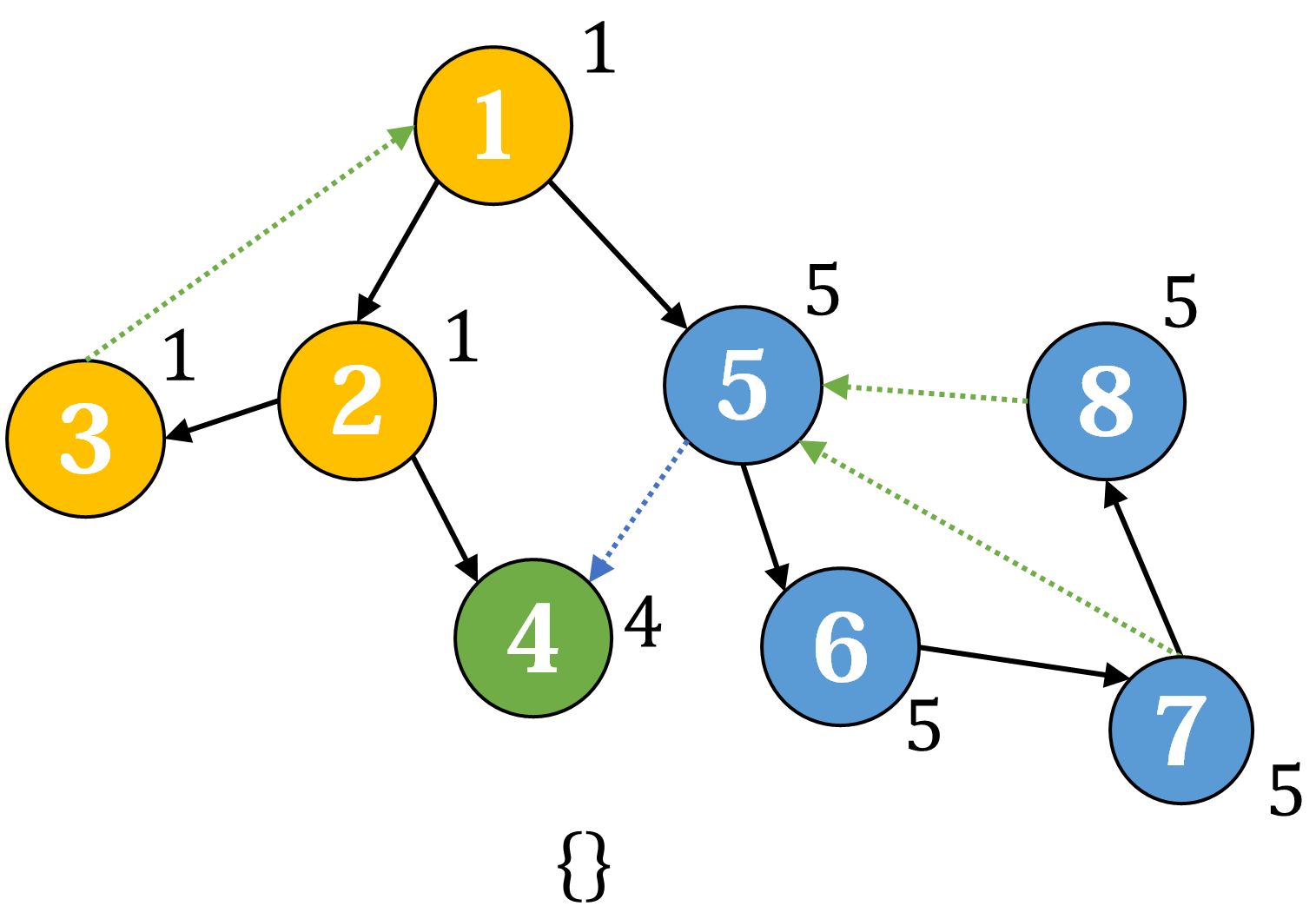
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| stack <int> stk;
int dfsn[N], low[N], instk[N], scc[N], cnt, scccnt;
void Tarjan (int p)
{
low[p] = dfsn[p] = ++ cnt;
instk[p] = 1;
stk.push (p);
for (auto q : edge[p])
{
if (!dfsn[q])
{
Tarjan (q);
low[p] = min (low[p], low[q]);
}
else if (instk[q])
low[p] = min (low[p], dfsn[q]);
}
if (low[p] == dfsn[p])
{
int top = -1;
scccnt ++;
while (top != p)
{
top = stk.top ();
stk.pop ();
instk[top] = 0;
scc[top] = scccnt;
}
}
}
|
注意,由于原图不一定是强连通图,所以不能随便找一个点作为根 就完事,而要保证每个点都被 到:
1
2
3
| for (int i = 1; i <= n; i ++)
if (!dfsn[i])
Tarjan (i);
|
时间复杂度是好像和 一样的 ,但是后者的常数更大,当然我也没拦着你用上面那个。
缩点
在求出强连通分量后,可以进行缩点,即:把处于同一个强连通分量的点当做同一个点处理。这样我们可以得到一张有向无环图。此外,注意到编号较小的点不能到达编号较大的点,于是 编号的顺序还符合拓扑序(编号越大的点拓扑序越靠前)。
1
2
3
4
| for (int u = 1; u <= n; u ++)
for (auto v : edge[u])
if (scc[u] != scc[v])
edges[scc[u]].push_back (scc[v]);
|
例如,在有向图中求经过的点权值之和最大的路径,就可以缩点,每个点的权值为缩之前的点的权值之和。这是因为如果一条路径经过强连通分量中的某个点,就可以经过其中的所有点。对于缩点后得到的有向无环图,可以按照拓扑序 。
再例如,求有向图中那些所有点都可达的点,也可以缩点,因为如果 可达 ,那么 所在的强连通分量中的所有点都可达 。对于得到的有向无环图,只需找到唯一出度为 的点即可。
Gabow
它其实和 的核心思想是差不多的,就是利用强连通分量必定是 的一棵子树这一重要性质,通过找出它的根来求解强连通分量,二者不同的是, 算法通过一个 数组来维护各个顶点能到达的最小前序编号;而 算法通过维护另一个栈来取代 数组,将前序编号值更大的顶点都弹出,然后通过栈顶的那个顶点来判断是否找到强连通分量的根,反正就是判断根的就是了(其实第二个栈内只会在找到一个强连通分量之前只会留下根)
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| void Gabow (int p)
{
dfsn[p] = ++ cnt;
stk.push (p);
root.push (p);
for (int i = 0; i < edge[p].size (); i ++)
{
int to = edge[p][i];
if (!dfsn[to])
Gabow (to);
else if (!scc[to])
{
while (dfsn[root.top ()] > dfsn[to])
root.pop ();
}
}
if (p == root.top ())
{
int top = -1;
root.pop ();
scccnt ++;
while (top != p)
{
top = stk.top ();
stk.pop ();
scc[top] = scccnt;
}
}
}
|
边双连通分量
结果给了张无向图,毛叼嘚,但是它们还是可以用 (是万金油吗),现在的问题转化成了边双连通分量(真会起名字)。
当两个点之间存在两条路径,且这两条路径包含的边完全不同时,这两个点属于同一边双,一个比较牛的性质就是没有割边。求法与有向图的强连通分量类似,在判返祖边的时候去掉走来当前点的那条边即彳亍,缩了边双之后图就变成了树(但是树不就是张图吗)。
我们从缩点的角度来看,你就知道了:
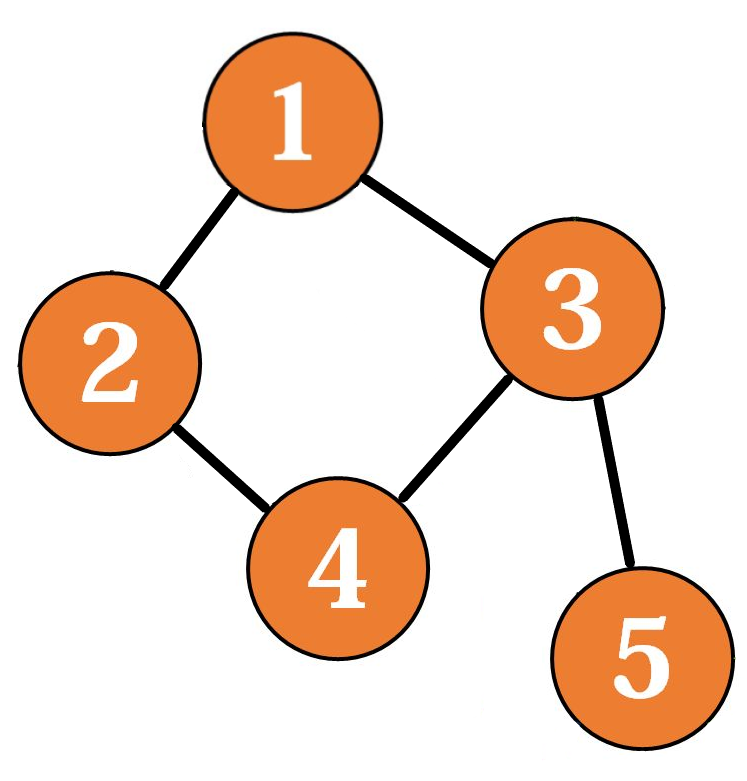
其中的 、 、 和 就是一个边双连通分量,那么经过缩点之后会变成这样( 表示里面有四个点):
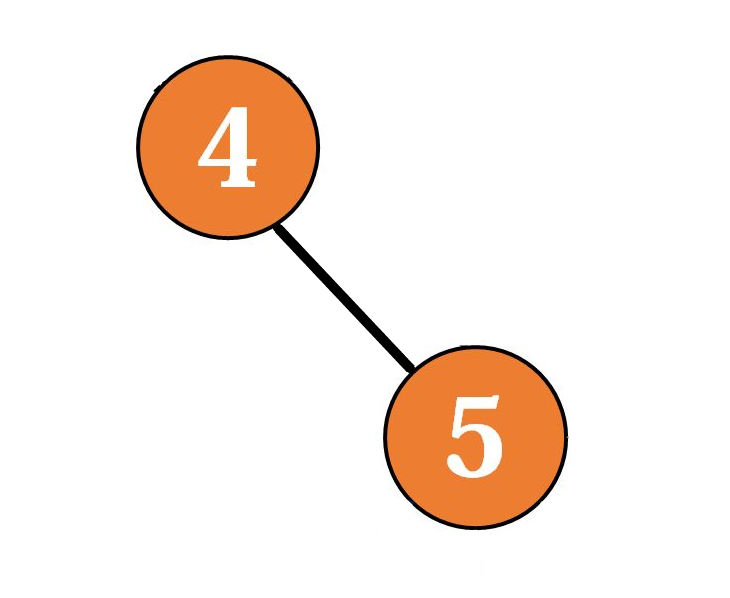
只需求出无向图中所有的割边,把割边都删除后,无向图会分成若干个连通块,每一个连通块就是一个边双连通分量。
最简单的方法就是先用 算法求出所有的桥,然后再对整个无向图执行一次 遍历(过程中不访问割边),划分出每个连通块即可。
但是记得我们前几秒说的吗,我们可以只加两行代码就可以完成以上繁琐的操作:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| void Tarjan (int p, int fath)
{
low[p] = dfsn[p] = ++ cnt;
instk[p] = 1;
stk.push (p);
for (auto q : edge[p])
if (q != fath)
{
if (!dfsn[q])
{
Tarjan (q, p);
low[p] = min (low[p], low[q]);
}
else if (instk[q])
low[p] = min (low[p], dfsn[q]);
}
}
if (low[p] == dfsn[p])
{
int top = -1;
scccnt ++;
while (top != p)
{
top = stk.top ();
stk.pop ();
instk[top] = 0;
scc[top] = scccnt;
}
}
}
|
点双连通分量
好家伙,我以为结束了,本来就很难了,真是三个愿望一次满足。
当两个点之间存在两条路径,且这两条路径所包含的点(除了端点)完全不同时,这两个点属于同一点双,这里主要讲割点求法(怎么用完割边用割点,和双子向日葵似的)。
对于根节点,如果有两棵以上的子树,就是割点。因为如果去掉这个点,这两颗子树就不能互相到达;对于非根节点,我们维护两个数组 和 (是不是很熟悉,如果觉得陌生就回溯到上面去看看吧)。然后给一个很简单但是很让人不解的结论就是:对于一条边 ,如果 ,此时 就是割点。
如果这个点是第一次被访问,那么进栈,当确定是鸽点(是接受送信任务的点)时,无论边的起点 是否为根,都要从栈顶不断弹出节点,直至边的终点 被弹出,刚才弹出的所有节点与这个起点 构成一个点双连通分量。
那其实也是用 去写,只不过这时我们要用到上面的结论罢了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| void Tarjan (int p)
{
dfsn[p] = low[p] = ++ cnt;
stk.push (p);
if (p == S && head[p] == 0)
{
dcc[++ dcccnt].push_back[x];
return ;
}
int flag = 0;
for (auto q : edge[p])
{
if (!dfsn[q])
{
Tarjan (q);
low[p] = min (low[p], low[q]);
if (low[q] >= dfsn[p])
{
flag ++;
if (x != S || flag > 1)
cut[p] = true;
cutcnt ++;
int temp = -1;
while (temp != q)
{
temp = stk.top ();
stk.pop ();
dcc[cnt].push_back (temp);
}
}
else
low[x] = min (low[x], dfsn[y]);
}
}
}
|













