欧拉图的新娘

所以我希望你不是为了别人而选择，而是思考自己想怎么做。——《魔法使的新娘》

你看这个欧拉图，就像森林一样。

欧拉图

欧拉图是指通过图（无向图或有向图）中所有边且每边仅经过一次通路，相应的回路成为欧拉回路，具有欧拉回路的图叫做欧拉图，具有欧拉路径而无欧拉回路的图称为半欧拉图，两张半欧拉图就可以合成一个欧拉图。欧拉图现代的扩展是蜘蛛图（也就是雷达图），它向欧拉图增加了可以连接的存在点。之前欧拉图只有合取特征（就是区定义了有着与起来的那些性质的对象在区中的存在，但是这和我们没有关系），这给予了它析取特征。

也可以说欧拉图就是从任意一个点开始都可以一笔画完整个图，半欧拉图必须从某个点开始才能一笔画完整个图。

欧拉图的诞生源于柯尼斯堡（加里宁格勒）的一条普雷格尔河，你听说过七桥问题吗？

好了你已经可以解决七桥问题了，这篇文章就这么结束吧。

七桥问题

世纪东普鲁士的柯尼斯堡，有一条河穿过了全城，河上有两个小岛，有七条桥把两个岛与河岸联系起来，一个不行者怎样才能不重复，不遗漏的一次走完七条桥，最后回到出发点。

那么我们的欧哥基于此提出了我们都玩过的“一笔画”，也就是欧拉回路。

当然已经在 世纪的我们知道应该是不可能的了基本大概。

给出一张欧拉图：

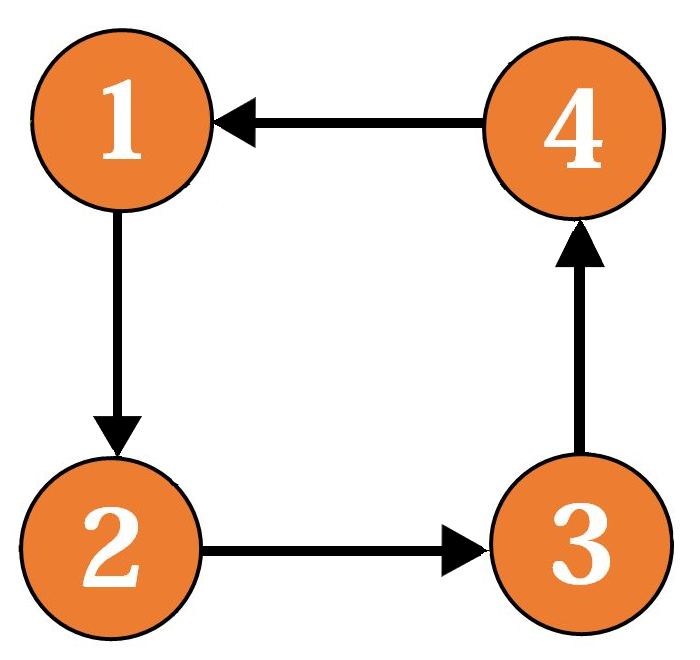
发现什么了吗？

不行，如果你没发现我也要告诉你了，我们可以发现欧拉图的一些性质（诶我没告诉你是要找性质吗）。

比较可以看出来的就是欧拉图里点的度数都是偶数，因为进出次数一定相等。

那么我们不一定可以知道半欧拉图是恰有 个或 个奇度顶点的。

在欧拉图中，当所有顶点属于同一个强连通分量的时候，每个顶点的入度和出度是相同的。但是半欧拉图果然是不同于欧拉图，将半欧拉图中的有向边退化成无向边的时候，这张图的所有点属于一个强连通分量，除了两个顶点外，其余顶点的出度和入度都是相等的，那两个顶点中一个顶点的入度和出度差为 ，另一个顶点的入度和出度差为 。

通过图中所有边恰好一次且行遍所有顶点的通路为欧拉路径（也可以叫做欧拉通路）。

欧拉回路

Fleury

也称避桥法，是一种比较暴力的算法，时间复杂度为糟糕的 ，实用性不高，再复杂一点实现需要用到动态图，实用价值不高，所以我们肯定不会讲它。

算法流程是每次选择下一条边的时候优先选择不是桥的边。

一个比较错误的方式就是先 预处理出桥，然后再 避桥，但是因为遍历过程中边会被删去，一些非桥边会变成桥边导致一些不可预估的错误，简单的实现方式是每次删除一条边之后暴力跑一遍 找桥更加稳妥，至于时间复杂度吗，跑 遍 （不知道 的可以溜去《分量大师 强连通女孩》去偷瞄一眼有意思的 ，然后你就会高兴地跑回来告诉我你没看到 的时间复杂度是 。

Hierholzer

是逐步插入回路法，又叫圈套圈算法。

算法流程是从一条回路开始，每次任取一条目前回路中的点，将其替换成一条简单回路，以此寻找到一条欧拉回路，如果从路开始的话，就可以寻找到一条欧拉路径。

开始时任选 中的一个顶点 ，从它开始跑 ，通过未访问过的边遍历相邻的点，等到无法遍历了就加入到一个路径数组里，一直到所有的边都被访问，此时路径数组的反序就是所求的欧拉回路。

代码如下：

void Hierholzer (int p)
{
	for (int i = edge[p]; i; i = edge[i].nxt)
	{
		int q = edge[i].to;
		if (vis[i])
		{
			vis[i] = false;
			vis[i ^ 1] = false; // 如果是反向边还要同时标记，如果没有就可以不用了哟 
			Hierholzer (q);
		}
	}
	s.push (p);
}

找张图来模拟一下过程：

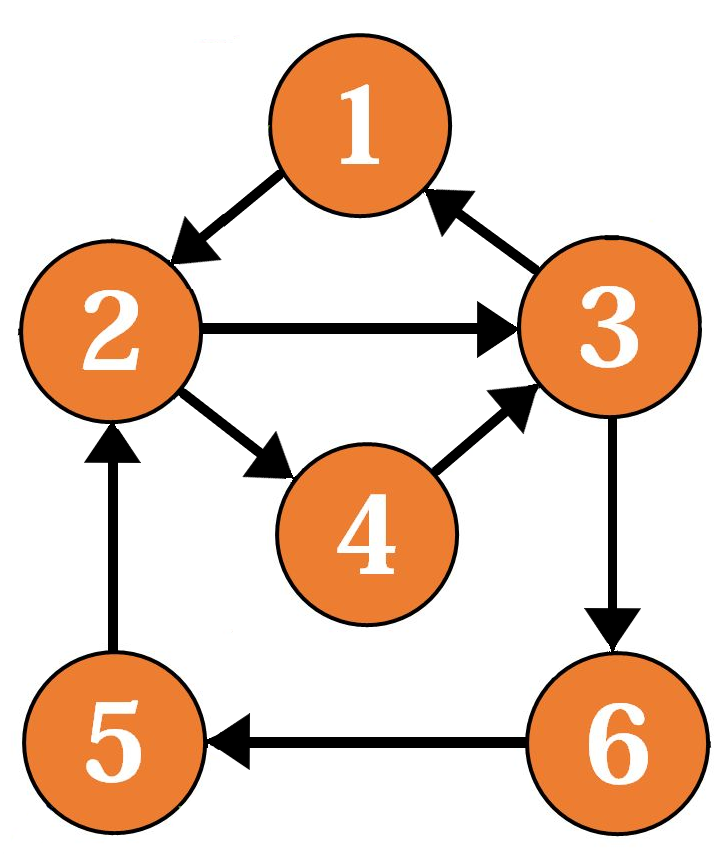
假设我们现在从 号点开始遍历：

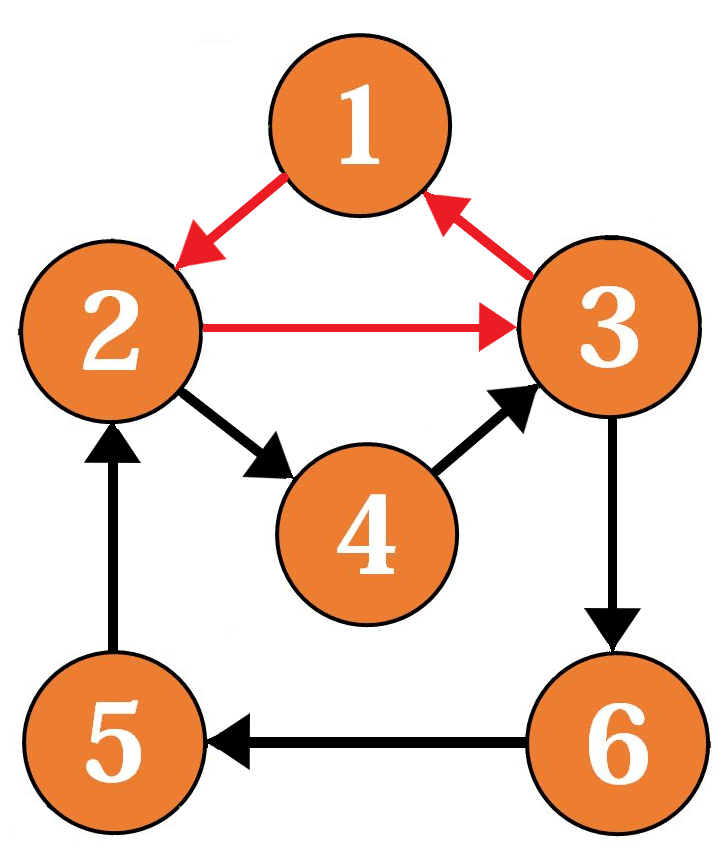
那么往后退到 号点，之后就可以好好遍历了：

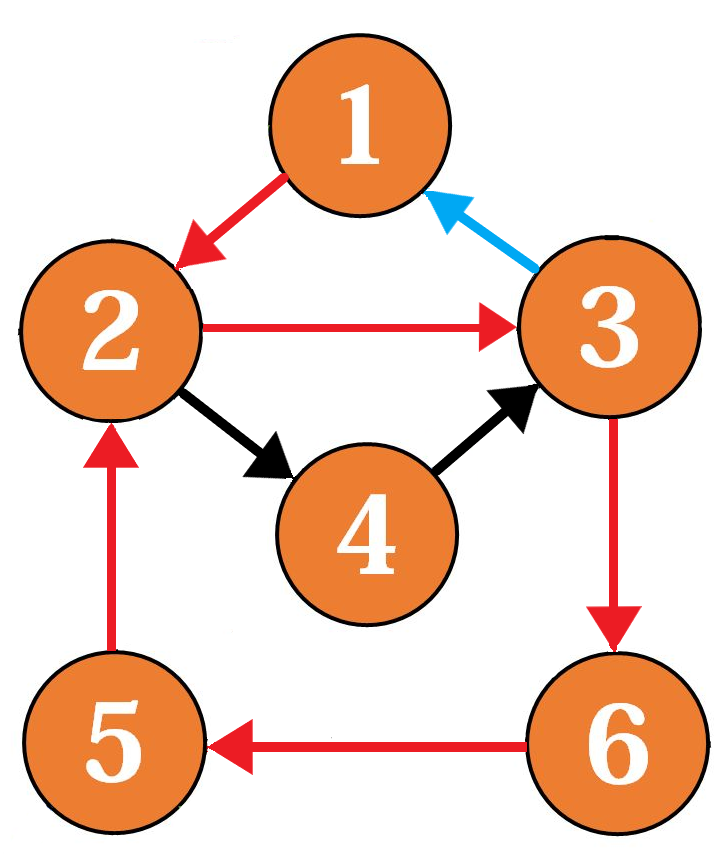
蓝色表示一条回路但是走到底了走不了了。

当然也可以写成邻接矩阵的形式：

void Hierholzer (int p)
{
	for (int i = 1; i <= n; i ++)
		if (mp[p][i])
		{
			mp[p][i] --;
			mp[i][p] --;
			Hierholzer (i);
		}
	s.push (p);
}