这股力量，到底是神还是恶魔呢？——《天才麻将少女》

逆元

在数论中，如果 ，我们就说 和 在模 意义下互为乘法逆元，记作 。

常常遇到一些题目要求对一个大质数 取模，加减法和乘法对取模运算都是封闭的，所以可以处处取模来避免溢出。

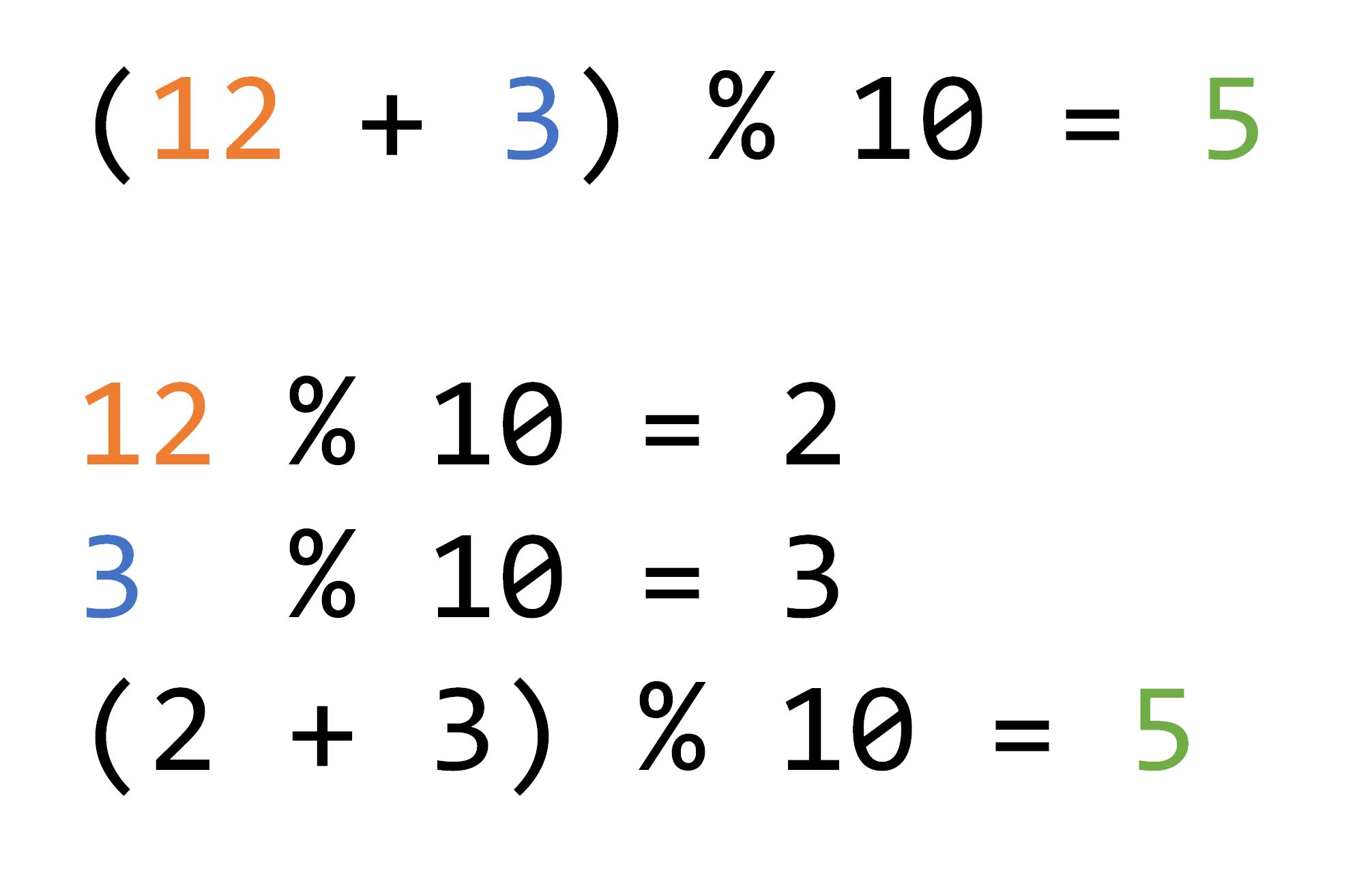
完全没有关系

可以看到，一次取模和步步取模的结果是一样的。

但遇到了除法，那就是小偷碰到了流氓：

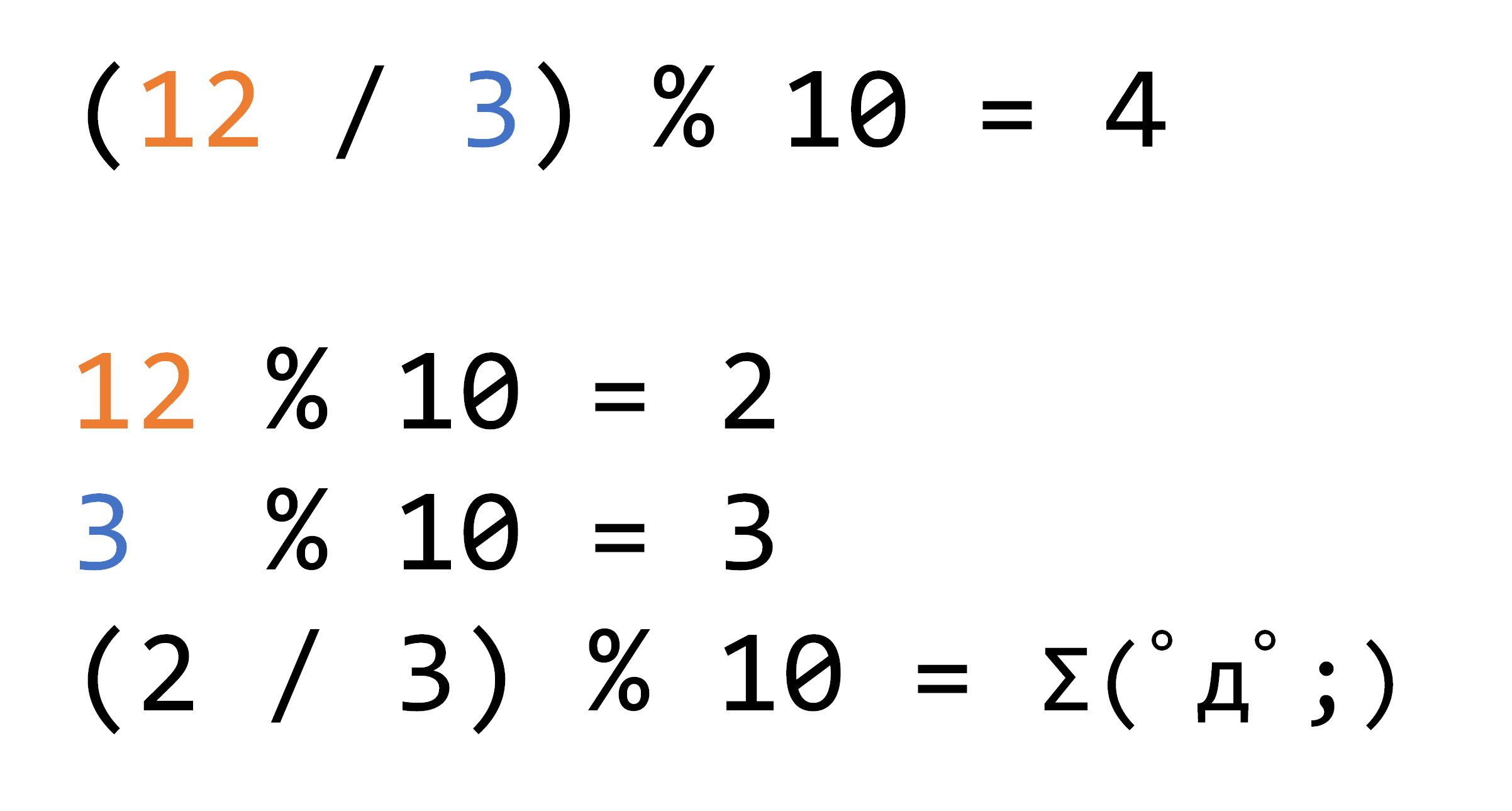
完全有关系

为了解决模意义的除法问题，我们引入了逆元。 其实可以看做模 意义下的 ，那么在模 意义下， 就可以变形为 。

那么综上所述，我们可以推出这么个不是东西的东西：

实际上，在模 意义下 ，所以上面的式子可以这样计算：

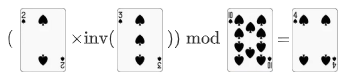
放错了，是这个：

和上面的不一样的道理么

所以这里介绍三种计算逆元的方法。

拓展欧几里得

同余方程实际上就是在求逆元，所以这就是常用的求逆元的方法。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int exgcd (int a. int b, int &x, int &y) // 扩展欧几里得算法  
{
	if (b == 0)
	{
		x = 1;
		y = 0;
		return a;
	}
	int d = exgcd (b, a % b, y, x);
	y -= (a / b) * x;
	return d;
}
int inv (int a, int p) // 欧几里得求逆元  
{
	int x, y;
	if (exgcd (a, p, x, y) != 1) // 无解情形 
		return -1;
	return (x % p + p) % p; // 模完可能出现负数所以再加一遍模一遍 
}

费马小定理

费马还是改个名吧，改叫费金花，费羊费牛费猪也比这个好听。风大了可不能走到街上，广告牌一砸下来，别人说，“哟，砸金花了”。

开个玩笑，纯属是个段子，配合一下我们的主题，各位可能知道费马大定理，费马中定理和费马超大定理，但是应该不知道这个。

费马小定理是数论里的重要定理，叙述如下：

若 是质数，且 ，则有 。

从逆元的定义拉倒，可得到 于是有 。

于是对 算一下快速幂就好了。注意，这个方法只对 为质数时的情况有效。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
inline int qpow (int b, int p, int mod) // 慢速幂 
{
	int res = 1;
	while (p)
	{
		if (p & 1)
			res = res * b % mod;
		b = b * b % mod;
		n >>= 1;
	}
	return res;
}
inline int inv (int a, int mod) // 费金花求逆元 
{
	return qpow (a, mod - 2, mod); // 费羊牛猪小定理 
}

有没有费马超小定理啊。

线性递推

虽然上面很常用，但是仍然过不了模板题。

所以我们这里介绍逆元的线性递推求法（要求 是质数）。

设：

即：

在模 意义下，有：

移项后得到：

则：

然后去把上面的两个式子代入，即：

其实和拓展欧几里得还是有不少相似之处的，可以用记忆化搜索的方法，减少多次查询的时间复杂度（递推即可）。

插播一个悲报：我在准备写这段代码的时候一个没拿稳把驼奶倒进键盘了（哭），等我先清理下键盘先。

回来了，我们继续写代码吧：

1
2
3
4
5
6
7
8
9
10
11
12
int Inv[n] = {0, 1};
inline int mod (int a, int p)
{
	return (a % p + p) % p;
}
int inv (int a, int p)
{
	if (Inv[a])
		return Inv[a];
	Inv[a] = mod (-p / a * Inv (p % a, p), p);
	return Inv[a];
}